一点透視

本章ではまず一点透視のモデルを説明し，つぎに実際の下描きを用いてカメラ座標を算出して，最後にBlender上に配置する手順を示します．

一点透視のモデル

本節では，一点透視のモデルを示した後， モデル上の点を座標軸上で移動させると，ある一点(消失点)に収束する振る舞いについて説明します．

任意の点\(G\)をカメラ\(C\)から見たときに，\(x=0\)にあるパネル\(P\)に映る座標\(Q\)を考えます． \(Q\)は\(\overrightarrow{GC}\)上のどこかなので，係数を\(u\)とおいて整理します．

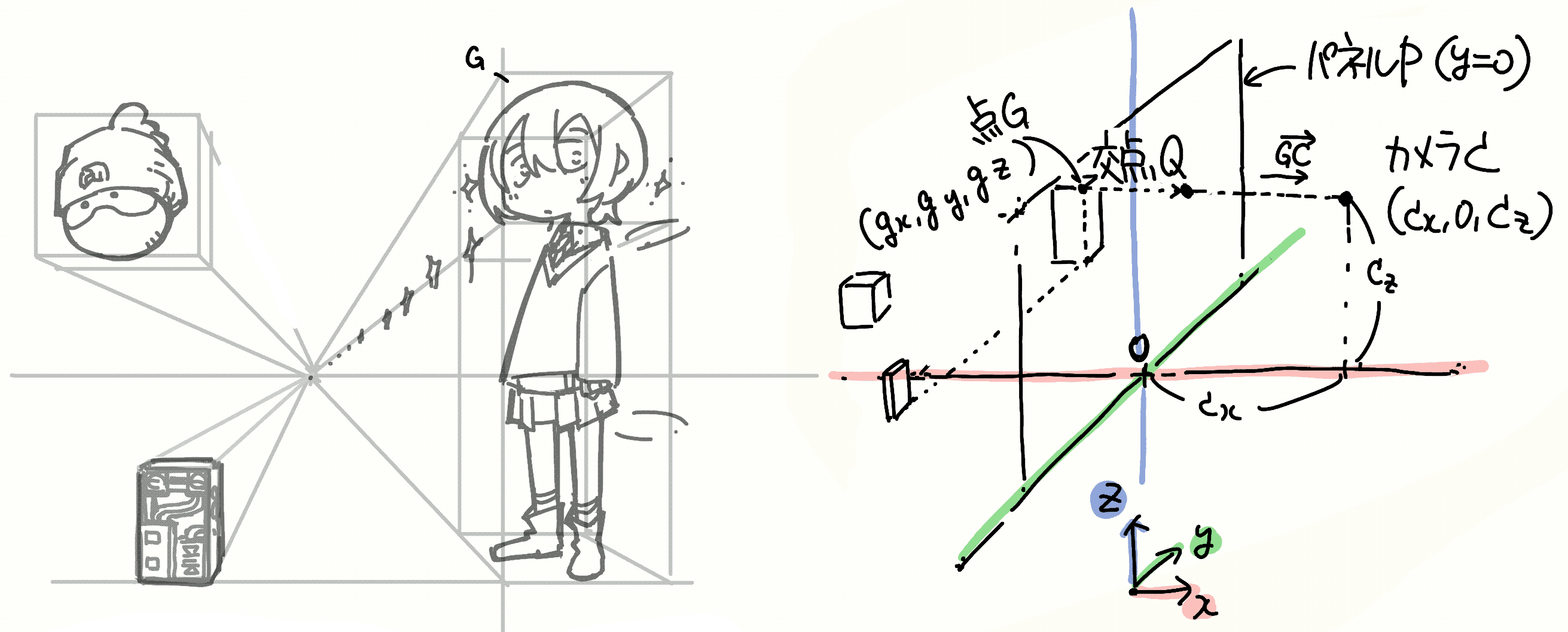
\[ \begin{eqnarray} \vec{Q} &=& u\overrightarrow{GC} \\ \begin{pmatrix} 0 \\ q_\mathrm{y} \\ q_\mathrm{z} \end{pmatrix} &=& \begin{pmatrix} g_\mathrm{x} \\ g_\mathrm{y} \\ g_\mathrm{z} \end{pmatrix} + u \begin{pmatrix} c_\mathrm{x} - g_\mathrm{x} \\ -g_\mathrm{y} \\ c_\mathrm{z} - g_\mathrm{z} \end{pmatrix} \\ u &=& \frac{g_\mathrm{x}}{g_\mathrm{x} - c_\mathrm{x}} \end{eqnarray} \] これを元の\(Q\)に代入して次式を得ます． \[ \vec{Q} = \begin{pmatrix} 0 \\ g_\mathrm{y} + \frac{g_\mathrm{x}g_\mathrm{y}}{c_\mathrm{x} - g_\mathrm{x}} \\ g_\mathrm{z} - \frac{g_\mathrm{x}(c_\mathrm{z} - g_\mathrm{z})}{c_\mathrm{x} - g_\mathrm{x}} \end{pmatrix} \]

軸に平行な移動

次に\(G\)を移動させたときの\(Q\)の振る舞いを考えます．まず奥行方向(x軸負の方向)へ移動させます． このときの左右方向は\(g_\mathrm{x} \to -\infty\)ですので，\(g_\mathrm{x}\)が分母となるように整理して \[ q_\mathrm{y} = g_\mathrm{y} + \frac{g_\mathrm{y}}{c_\mathrm{x} / g_\mathrm{x} - 1} \] よって \(g_\mathrm{x} \to -\infty\)のとき\(q_\mathrm{y}=0\)となり，画面中央に収束することがわかります． 同様に高さは\(q_\mathrm{z} = c_\mathrm{z}\)となり，これはカメラの高さです． 上記より，消失点のy座標(左右)は画面の中央，z座標(上下)はカメラの高さとなることがわかります． なお，カメラのx座標については後述します．

なお，左右，または上下方向に動く点はいずれも発散しますのでパネルサイズで見切れることになります．

軸に対して傾きのある移動

前節の内容を一般化するために，軸に対して傾きのある移動をする場合を考えます． 簡単のために，まず傾きが45°(\(g_\mathrm{y} = -g_\mathrm{x},~ g_\mathrm{x} \to -\infty\))とすると 次式となります．

\[ \begin{eqnarray*} q_\mathrm{y} &=& -g_\mathrm{x} + \frac{-{g_\mathrm{x}}^2}{c_\mathrm{x} - g_\mathrm{x}} \\ &=& \frac{-c_\mathrm{x}g_\mathrm{x} + {g_\mathrm{x}}^2 - {g_\mathrm{x}}^2}{c_\mathrm{x} - g_\mathrm{x}} \\ &=& \frac{-c_\mathrm{x}}{c_\mathrm{x}/g_\mathrm{x} - 1} = c_\mathrm{x} \end{eqnarray*} \]

よって，少し恣意的ですがカメラのx座標\(c_\mathrm{x}\)を下記の手順で求めることができます．

1. 正方形を描いて対角線を伸ばす
2. 上記がカメラの高さとなる点(=通常の消失点から伸ばした水平線との交点)と，消失点との距離を求める

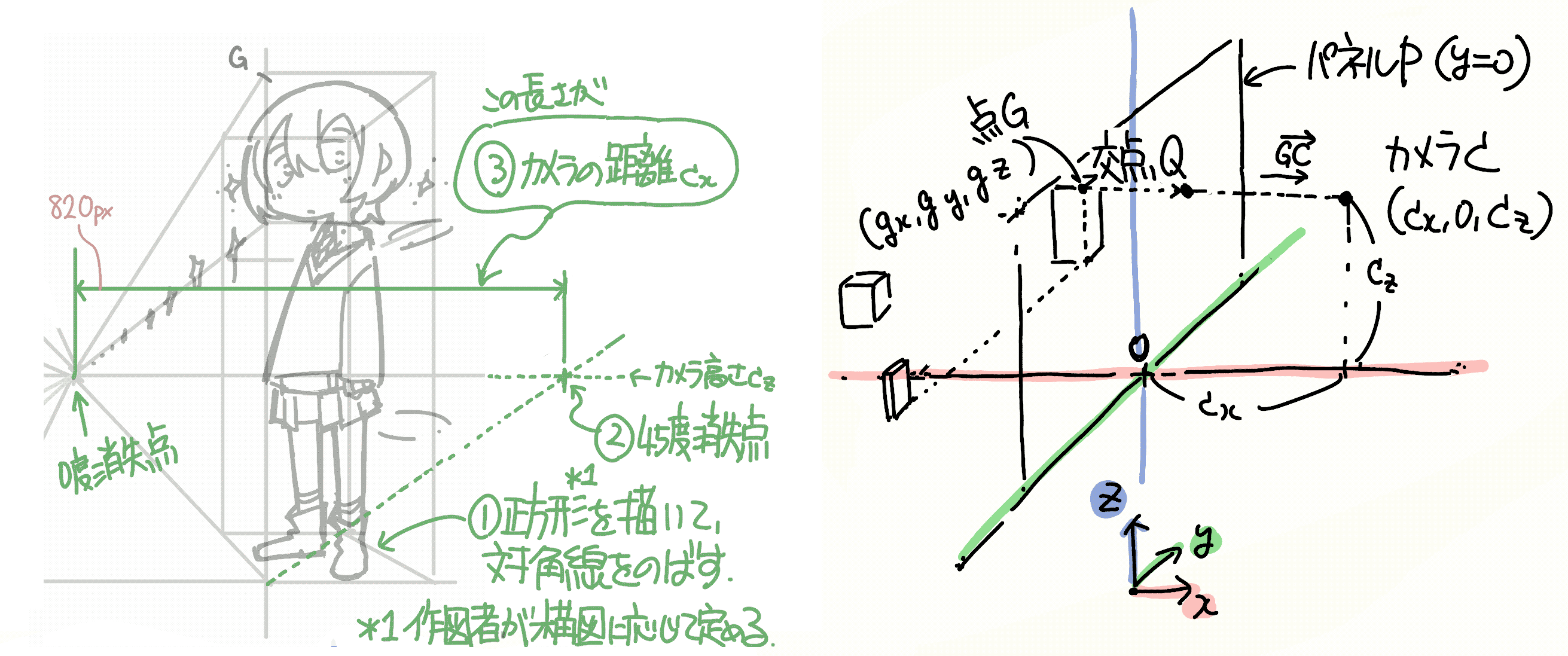
ここで，正方形に相当する台形の形状は作図者が任意に定めて構いません．その形状に応じてカメラのx座標が定まります． 逆に，カメラのx座標を定めると台形の形状が定まることになります．

Blenderでの操作

本節では，下記の画像を例として，整合するカメラ位置をBlender上に配置する手順を示します．

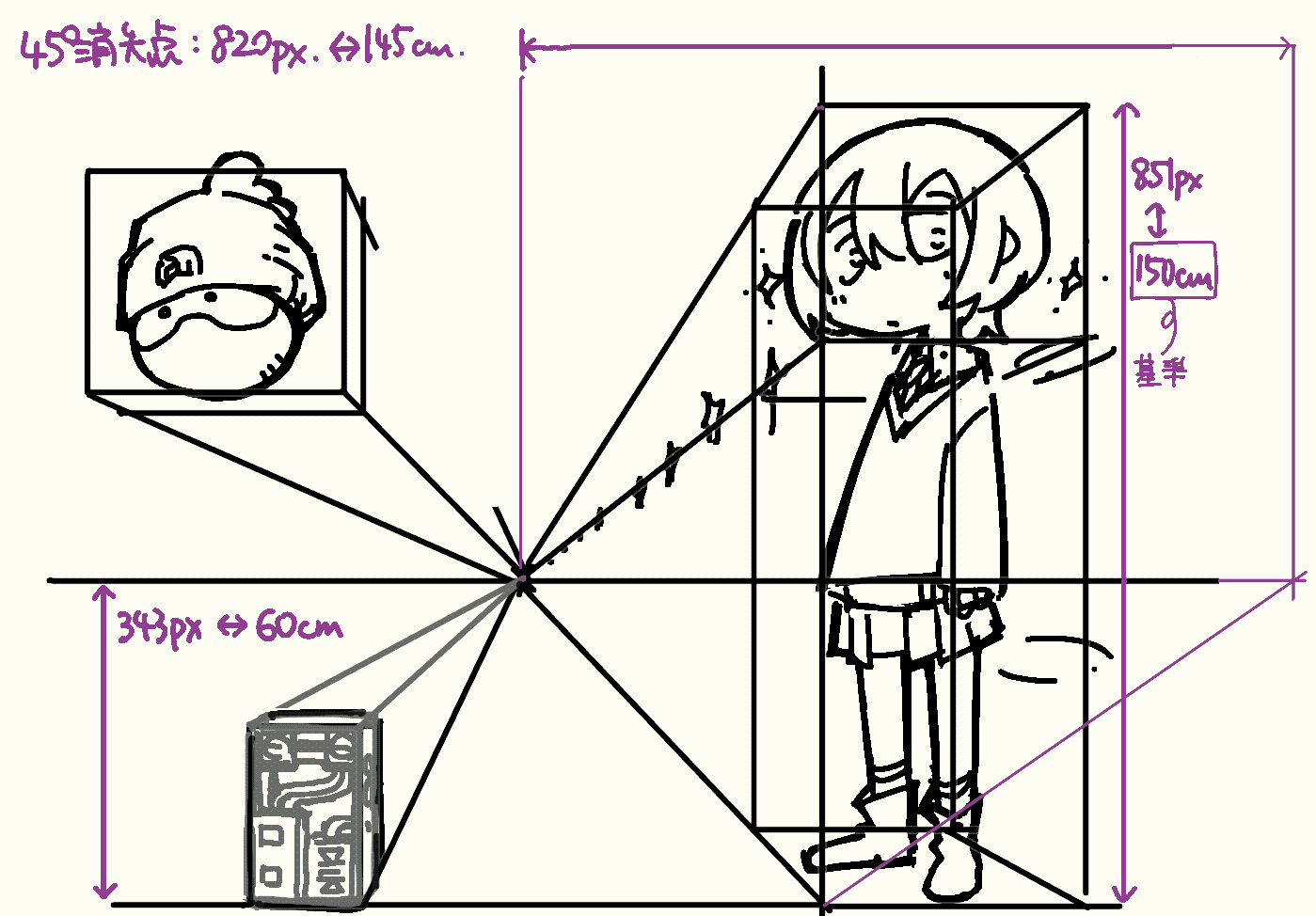
ここで，画像のピクセル数とBlenderでの寸法(メートル)を換算する計算をしておきます． 今回はキャラクター手前がパネルに接しているように描いています．そこで身長を150cmと仮定して，画像で851pxが150cmに対応するものとします． (基準になりそうなものがパネルに接していない場合は，一点透視図法でパネルに接する位置に移動して換算するとよいでしょう)．

次にカメラ座標を求めます．高さは下端から消失点まで，また，パネルからの距離は先程求めた45°消失点までの距離で， それぞれ343px(60cm)，820px(145cm)となりました．

手順	イメージ
(1) 下描きを表示するためにEmpty要素を追加します．
(2) このあとの操作で扱いやすいように下描きを仮配置します．ここでは原点に，90°/0°/90°としました．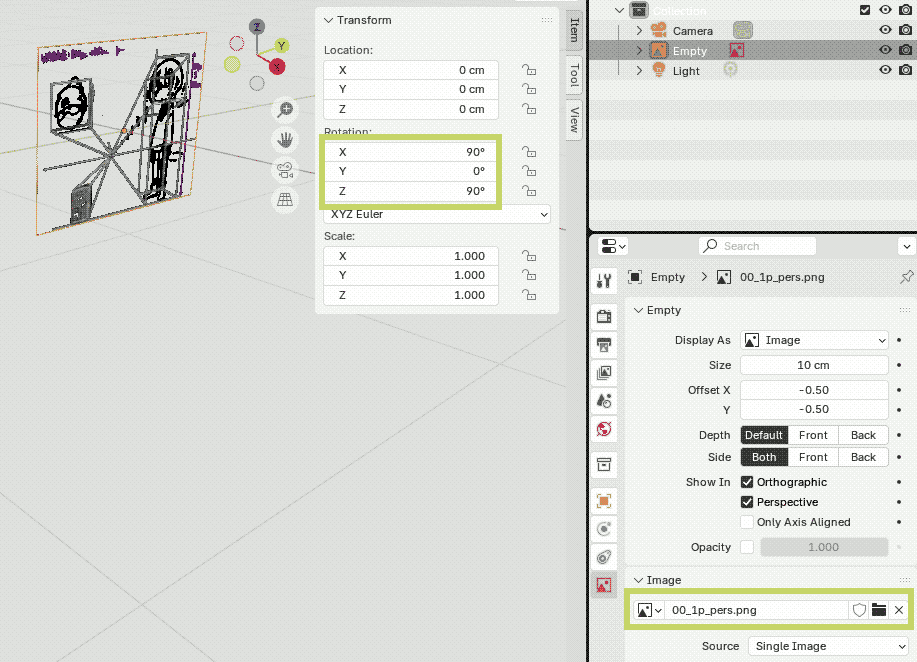
(3) 次に，下描きの拡大率を調整するための基準となるオブジェクト(Cube)を追加します．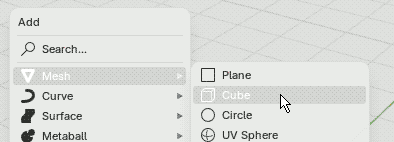
(4) ここではキャラクターの身長を150cmと仮定しました．なお，下描きの表示と重ならないように少し後ろにずらしています(x=-5.2cmの設定部分)．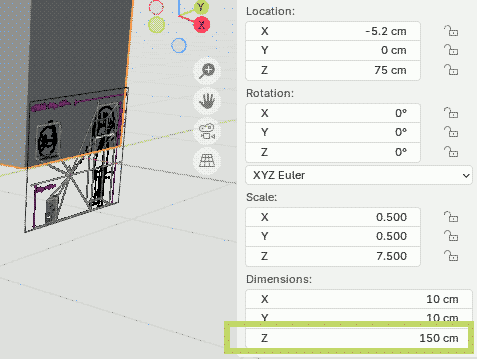
(5) 下描きの座標を調整します．Cubeは一旦非表示とした後，正面視点に設定します．まず左右を消失点に合わせ，次に上下を下端に合わせます．下端は任意に定めて構いません．今回はキャラクターの手前側がパネルに接していると定めました．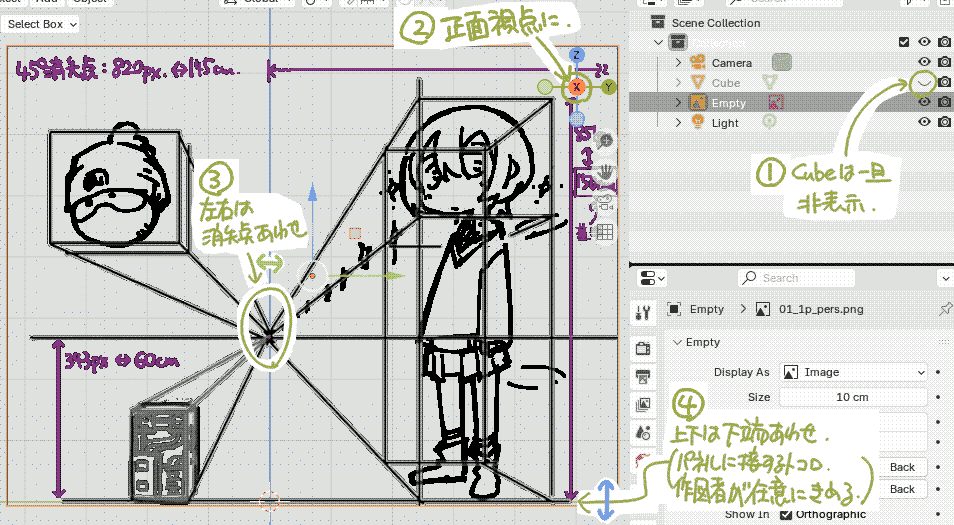
(6) 下描きを拡大操作する際の起点を設定します．まずPivotを3D Cursorに設定した後，3D Cursorを原点に設定します．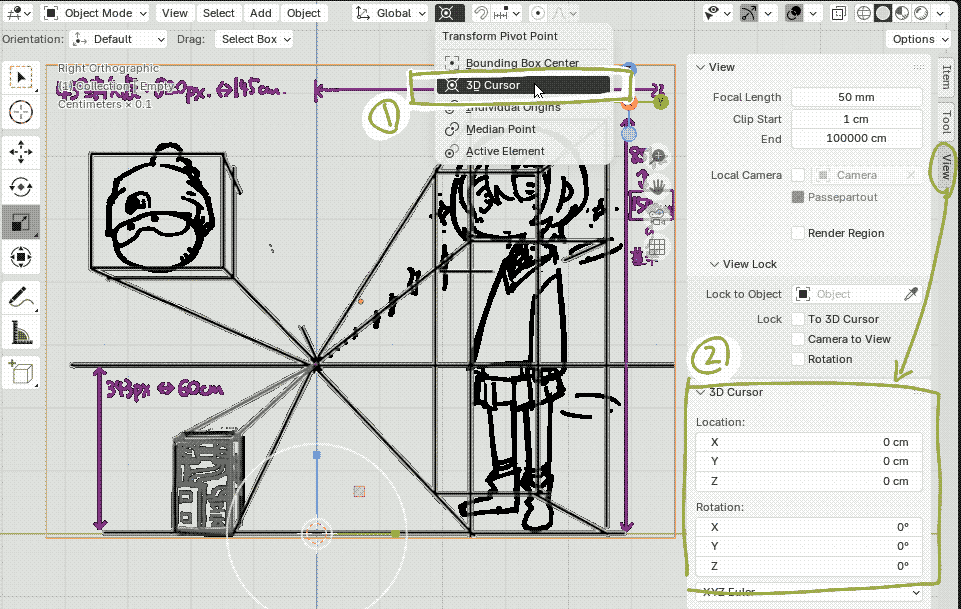
(7) キャラクターの上端が，先程配置したオブジェクトの状態と一致するように拡大します．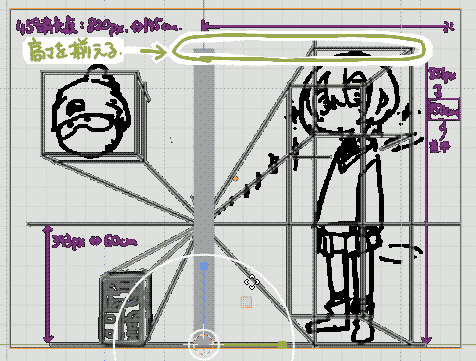
(8) 次に，先程計算した座標にカメラを配置します．また，方向を90°/0°/90°とします．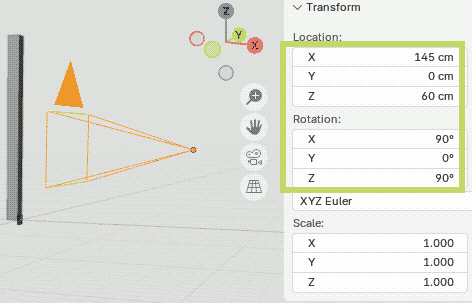
(9) 最後にカメラ視点に設定して，任意に配置したオブジェクトのx軸方向の傾きがx軸のグリッドに一致していればOKです． その後，ガイドにしたいオブジェクトを配置し，焦点距離とシフト量を調整してレンダリングします．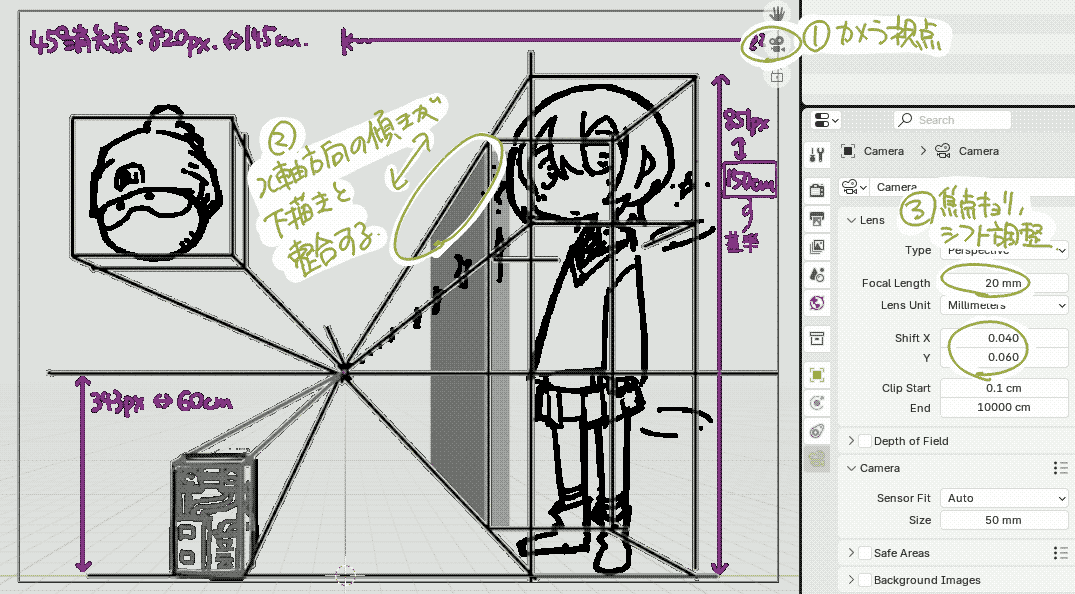

一点透視については以上です．続いて二点透視について説明します．