概要

本稿では，イラストや漫画における背景作画をBlenderなどの3D CADで効率化するための手順を紹介します．まず背景では，想定するユースケースを説明します．次に一点透視では，一点透視図法のモデル式を説明します．さらに下描きの例を用いてカメラ座標を算出し，Blender上に配置して検証します．二点透視，および三点透視では，一点透視と同様にモデルの説明，カメラ座標の算出，およびBlender上での検証について説明します．最後に，まとめにてまとめと所感について述べます．

背景

本章では背景と，想定するユースケースを説明します．

イラストや漫画の作画では，一般に透視図法が用いられます．透視図法では同じ軸方向に対して，ある長さがどのように変化するかを容易に得ることができます(下図(1))．また，異なる長さは対角線を利用した分割が有効です(下図(2))．しかしながら，異なる軸方向に対して同一の寸法を得る(下図(3)) 簡便な手法が，筆者が調べた範囲では見あたりませんでした．

そこで，作図的な方法でなく3D CADを活用した方法について検討します．筆者は同人誌の作成において下描きでおおよその構図を定めたあと背景を描き入れることが多いです．そこで以下のような手順を想定します．

手順	作業イメージ
1.人物などをメインに構図決め
2.妥当な位置にカメラを配置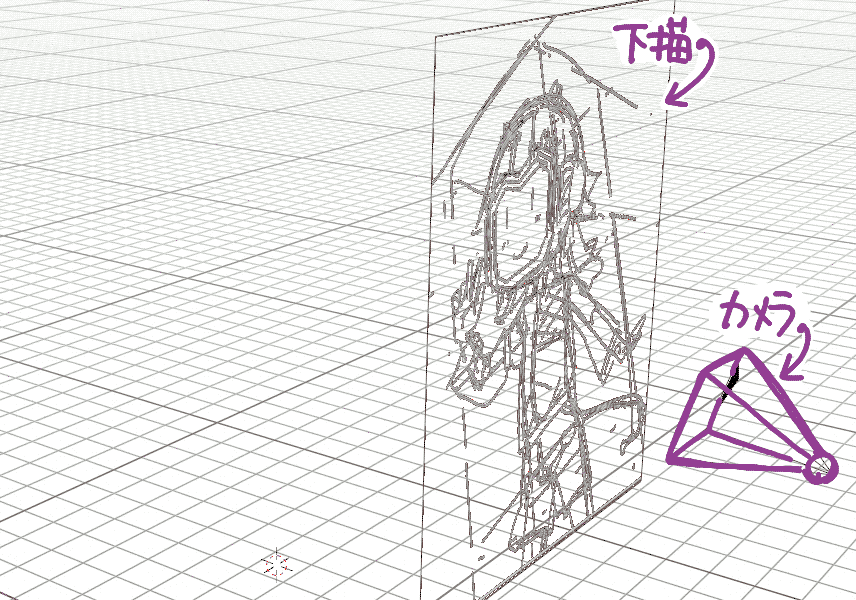
3.他のオブジェクトを配置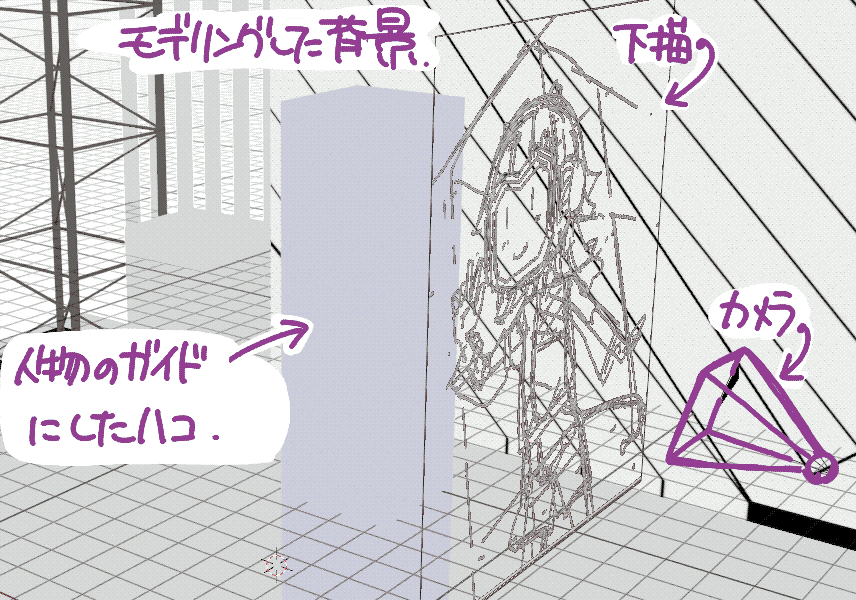
4.レンダリング

なお，理論的な背景，およびそれをもとに作図する方法については下記の資料¹が大変参考になりました．本稿で説明する内容の多くは，同じ著者さんの文献² ³ ⁴を参考にしています．体系的に整理された資料を公開いただいていることに心から感謝いたします．

本稿は，ほぼこれらの資料に対する筆者の読書メモではありますが，自身の理解のためと，もし同じところで悩んだ方の助けになればと思い執筆いたしました．

一点透視

本章ではまず一点透視のモデルを説明し，つぎに実際の下描きを用いてカメラ座標を算出して，最後にBlender上に配置する手順を示します．

一点透視のモデル

本節では，一点透視のモデルを示した後，モデル上の点を座標軸上で移動させると，ある一点(消失点)に収束する振る舞いについて説明します．

任意の点\(G\)をカメラ\(C\)から見たときに，\(x=0\)にあるパネル\(P\)に映る座標\(Q\)を考えます． \(Q\)は\(\overrightarrow{GC}\)上のどこかなので，係数を\(u\)とおいて整理します．

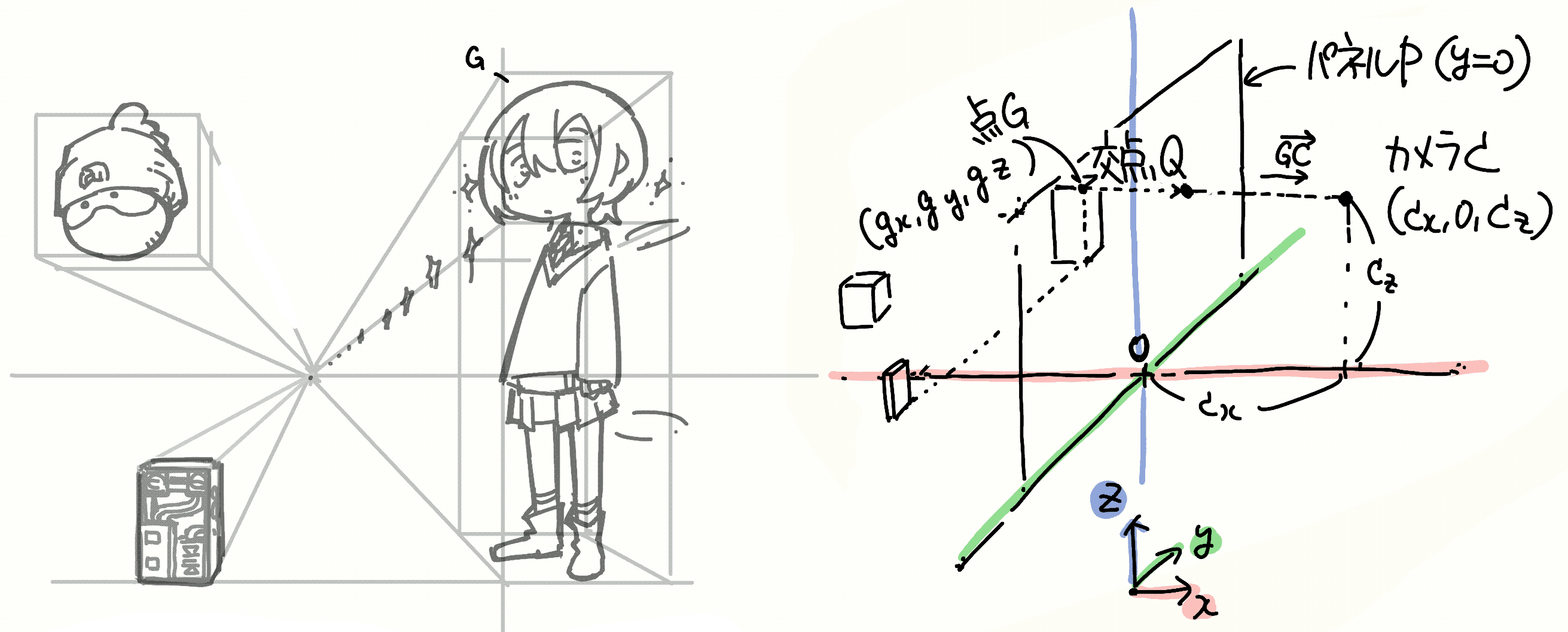
\[ \begin{eqnarray} \vec{Q} &=& u\overrightarrow{GC} \\ \begin{pmatrix} 0 \\ q_\mathrm{y} \\ q_\mathrm{z} \end{pmatrix} &=& \begin{pmatrix} g_\mathrm{x} \\ g_\mathrm{y} \\ g_\mathrm{z} \end{pmatrix} + u \begin{pmatrix} c_\mathrm{x} - g_\mathrm{x} \\ -g_\mathrm{y} \\ c_\mathrm{z} - g_\mathrm{z} \end{pmatrix} \\ u &=& \frac{g_\mathrm{x}}{g_\mathrm{x} - c_\mathrm{x}} \end{eqnarray} \] これを元の\(Q\)に代入して次式を得ます． \[ \vec{Q} = \begin{pmatrix} 0 \\ g_\mathrm{y} + \frac{g_\mathrm{x}g_\mathrm{y}}{c_\mathrm{x} - g_\mathrm{x}} \\ g_\mathrm{z} - \frac{g_\mathrm{x}(c_\mathrm{z} - g_\mathrm{z})}{c_\mathrm{x} - g_\mathrm{x}} \end{pmatrix} \]

軸に平行な移動

次に\(G\)を移動させたときの\(Q\)の振る舞いを考えます．まず奥行方向(x軸負の方向)へ移動させます．このときの左右方向は\(g_\mathrm{x} \to -\infty\)ですので，\(g_\mathrm{x}\)が分母となるように整理して \[ q_\mathrm{y} = g_\mathrm{y} + \frac{g_\mathrm{y}}{c_\mathrm{x} / g_\mathrm{x} - 1} \] よって \(g_\mathrm{x} \to -\infty\)のとき\(q_\mathrm{y}=0\)となり，画面中央に収束することがわかります．同様に高さは\(q_\mathrm{z} = c_\mathrm{z}\)となり，これはカメラの高さです．上記より，消失点のy座標(左右)は画面の中央，z座標(上下)はカメラの高さとなることがわかります．なお，カメラのx座標については後述します．

なお，左右，または上下方向に動く点はいずれも発散しますのでパネルサイズで見切れることになります．

軸に対して傾きのある移動

前節の内容を一般化するために，軸に対して傾きのある移動をする場合を考えます．簡単のために，まず傾きが45°(\(g_\mathrm{y} = -g_\mathrm{x},~ g_\mathrm{x} \to -\infty\))とすると次式となります．

\[ \begin{eqnarray*} q_\mathrm{y} &=& -g_\mathrm{x} + \frac{-{g_\mathrm{x}}^2}{c_\mathrm{x} - g_\mathrm{x}} \\ &=& \frac{-c_\mathrm{x}g_\mathrm{x} + {g_\mathrm{x}}^2 - {g_\mathrm{x}}^2}{c_\mathrm{x} - g_\mathrm{x}} \\ &=& \frac{-c_\mathrm{x}}{c_\mathrm{x}/g_\mathrm{x} - 1} = c_\mathrm{x} \end{eqnarray*} \]

よって，少し恣意的ですがカメラのx座標\(c_\mathrm{x}\)を下記の手順で求めることができます．

正方形を描いて対角線を伸ばす
上記がカメラの高さとなる点(=通常の消失点から伸ばした水平線との交点)と，消失点との距離を求める

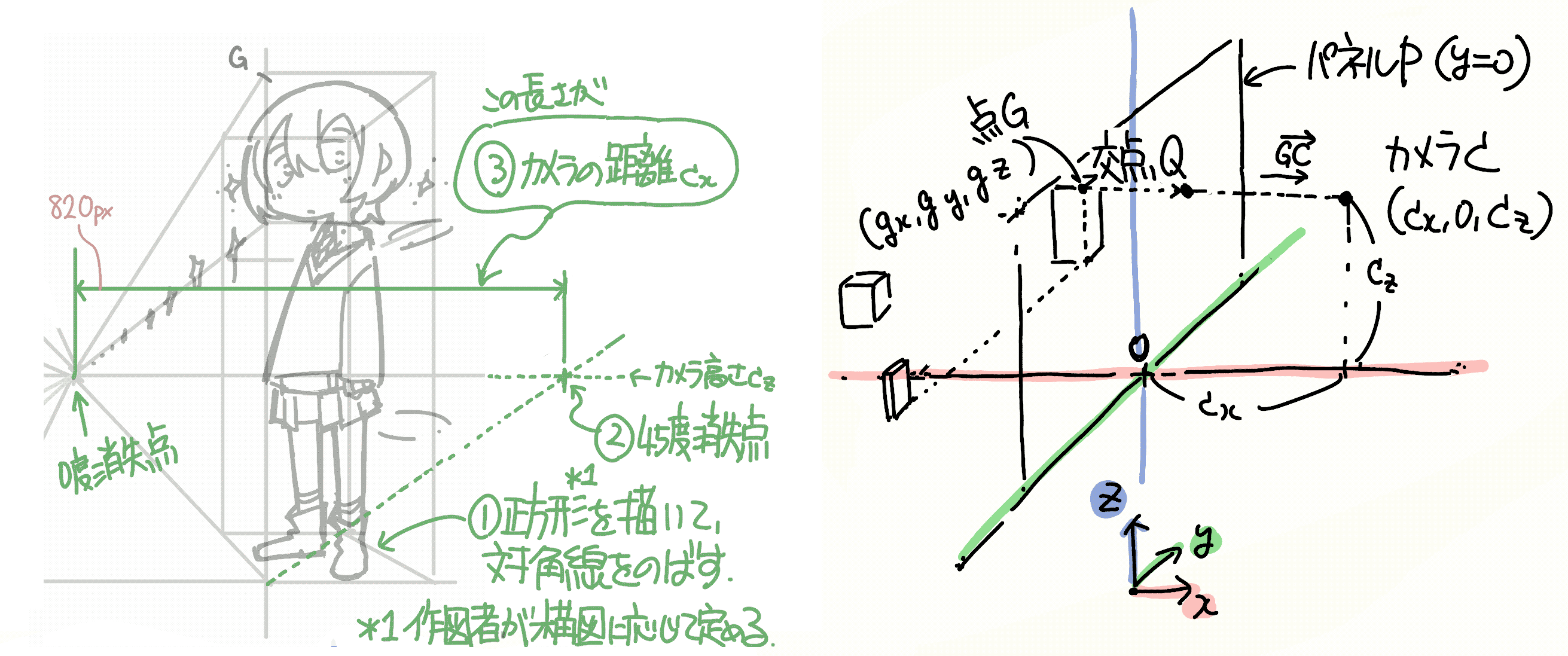
ここで，正方形に相当する台形の形状は作図者が任意に定めて構いません．その形状に応じてカメラのx座標が定まります．逆に，カメラのx座標を定めると台形の形状が定まることになります．

Blenderでの操作

本節では，下記の画像を例として，整合するカメラ位置をBlender上に配置する手順を示します．

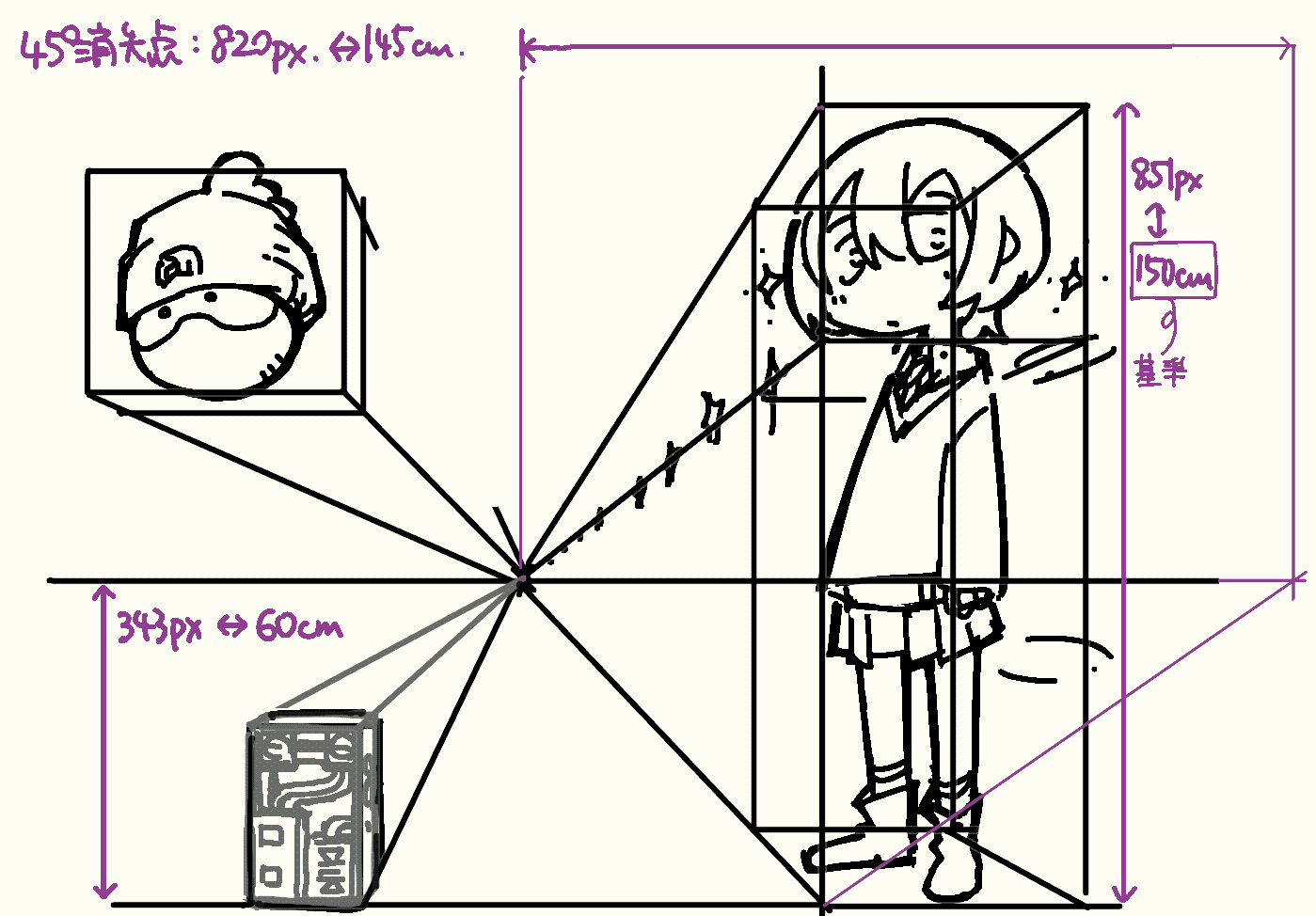
ここで，画像のピクセル数とBlenderでの寸法(メートル)を換算する計算をしておきます．今回はキャラクター手前がパネルに接しているように描いています．そこで身長を150cmと仮定して，画像で851pxが150cmに対応するものとします． (基準になりそうなものがパネルに接していない場合は，一点透視図法でパネルに接する位置に移動して換算するとよいでしょう)．

次にカメラ座標を求めます．高さは下端から消失点まで，また，パネルからの距離は先程求めた45°消失点までの距離で，それぞれ343px(60cm)，820px(145cm)となりました．

手順	イメージ
(1) 下描きを表示するためにEmpty要素を追加します．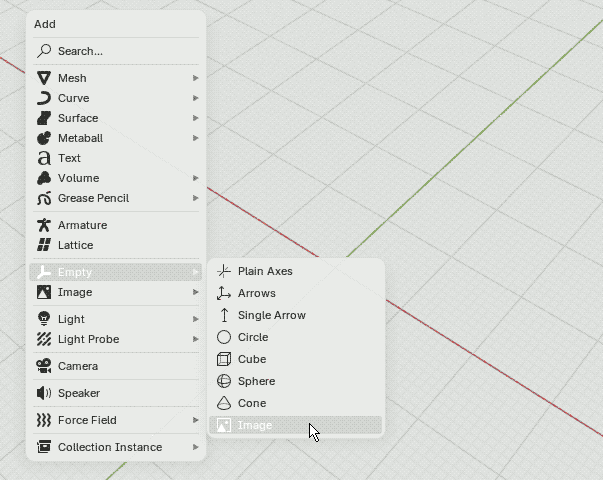
(2) このあとの操作で扱いやすいように下描きを仮配置します．ここでは原点に，90°/0°/90°としました．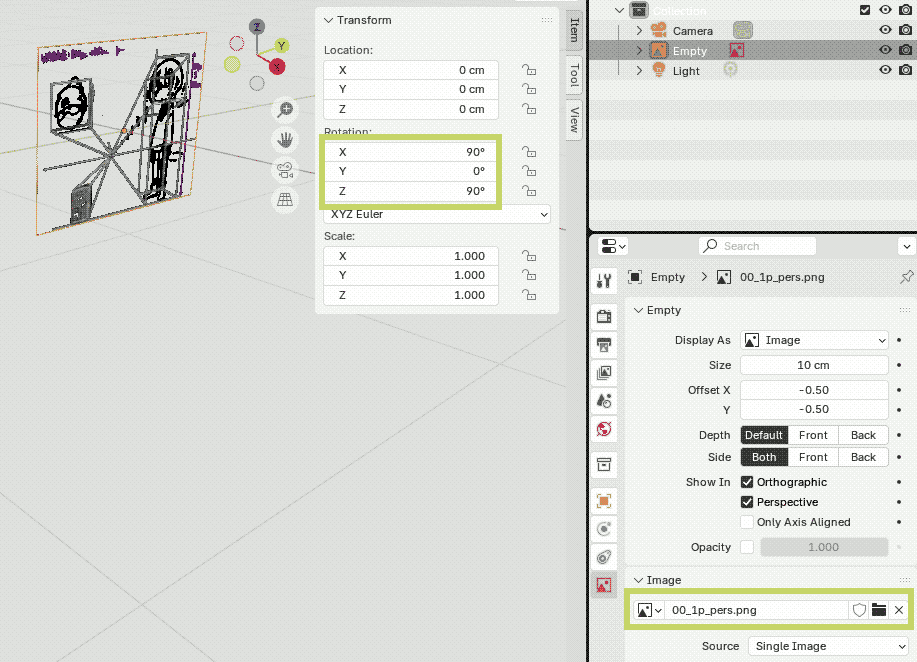
(3) 次に，下描きの拡大率を調整するための基準となるオブジェクト(Cube)を追加します．
(4) ここではキャラクターの身長を150cmと仮定しました．なお，下描きの表示と重ならないように少し後ろにずらしています(x=-5.2cmの設定部分)．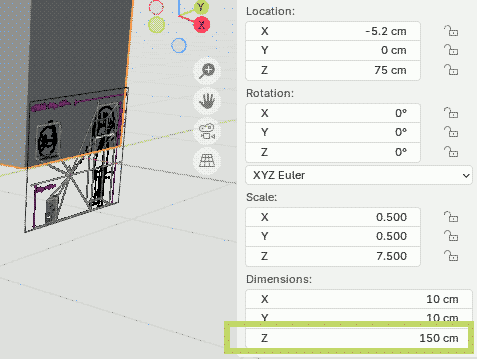
(5) 下描きの座標を調整します．Cubeは一旦非表示とした後，正面視点に設定します．まず左右を消失点に合わせ，次に上下を下端に合わせます．下端は任意に定めて構いません．今回はキャラクターの手前側がパネルに接していると定めました．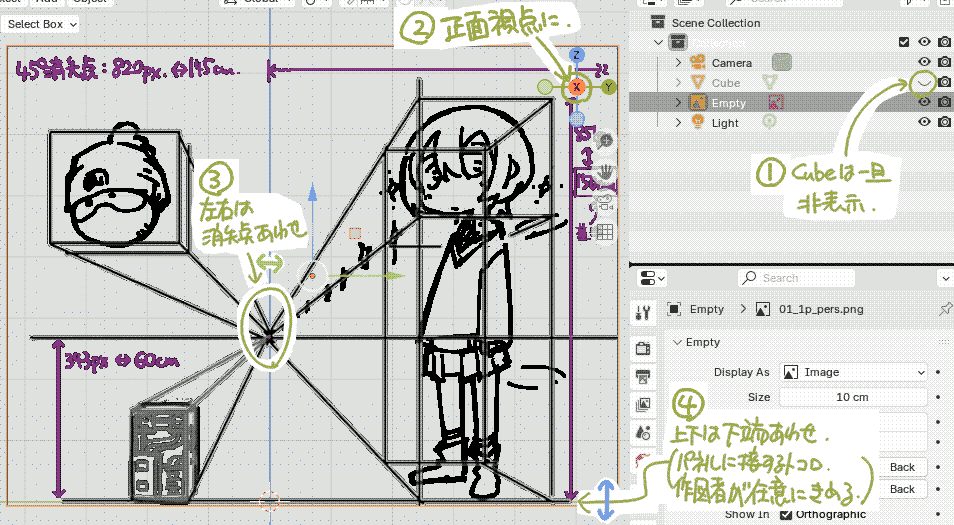
(6) 下描きを拡大操作する際の起点を設定します．まずPivotを3D Cursorに設定した後，3D Cursorを原点に設定します．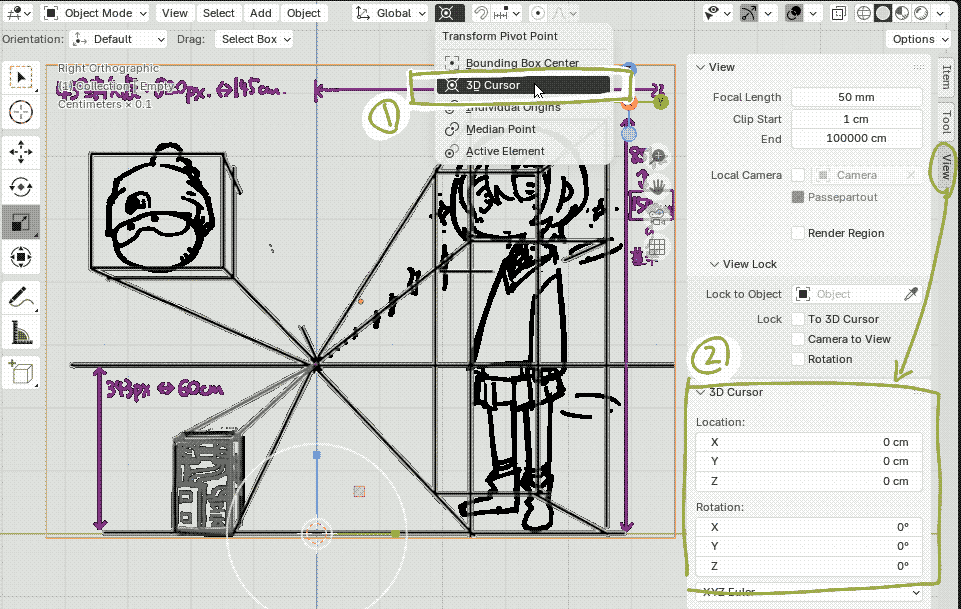
(7) キャラクターの上端が，先程配置したオブジェクトの状態と一致するように拡大します．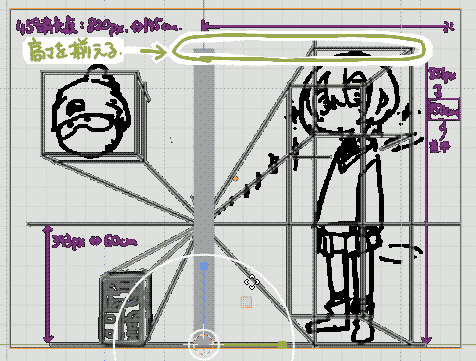
(8) 次に，先程計算した座標にカメラを配置します．また，方向を90°/0°/90°とします．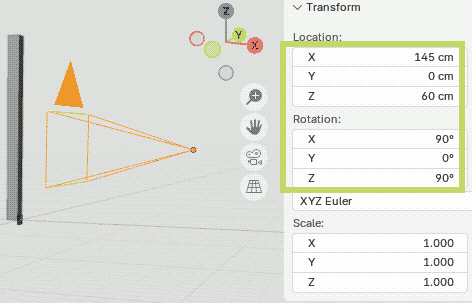
(9) 最後にカメラ視点に設定して，任意に配置したオブジェクトのx軸方向の傾きがx軸のグリッドに一致していればOKです．その後，ガイドにしたいオブジェクトを配置し，焦点距離とシフト量を調整してレンダリングします．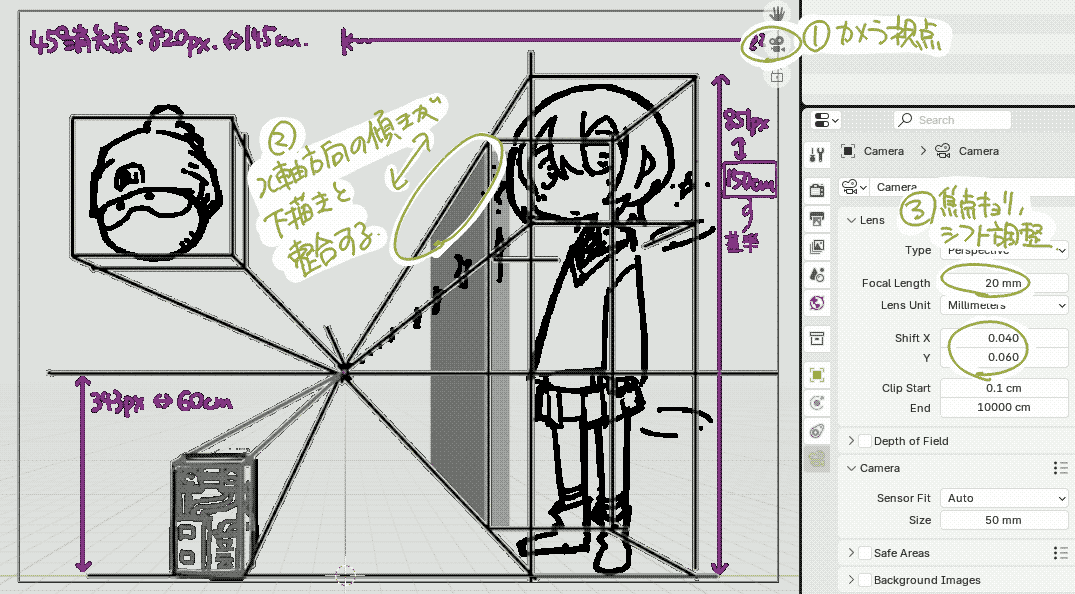

一点透視については以上です．続いて二点透視について説明します．

二点透視

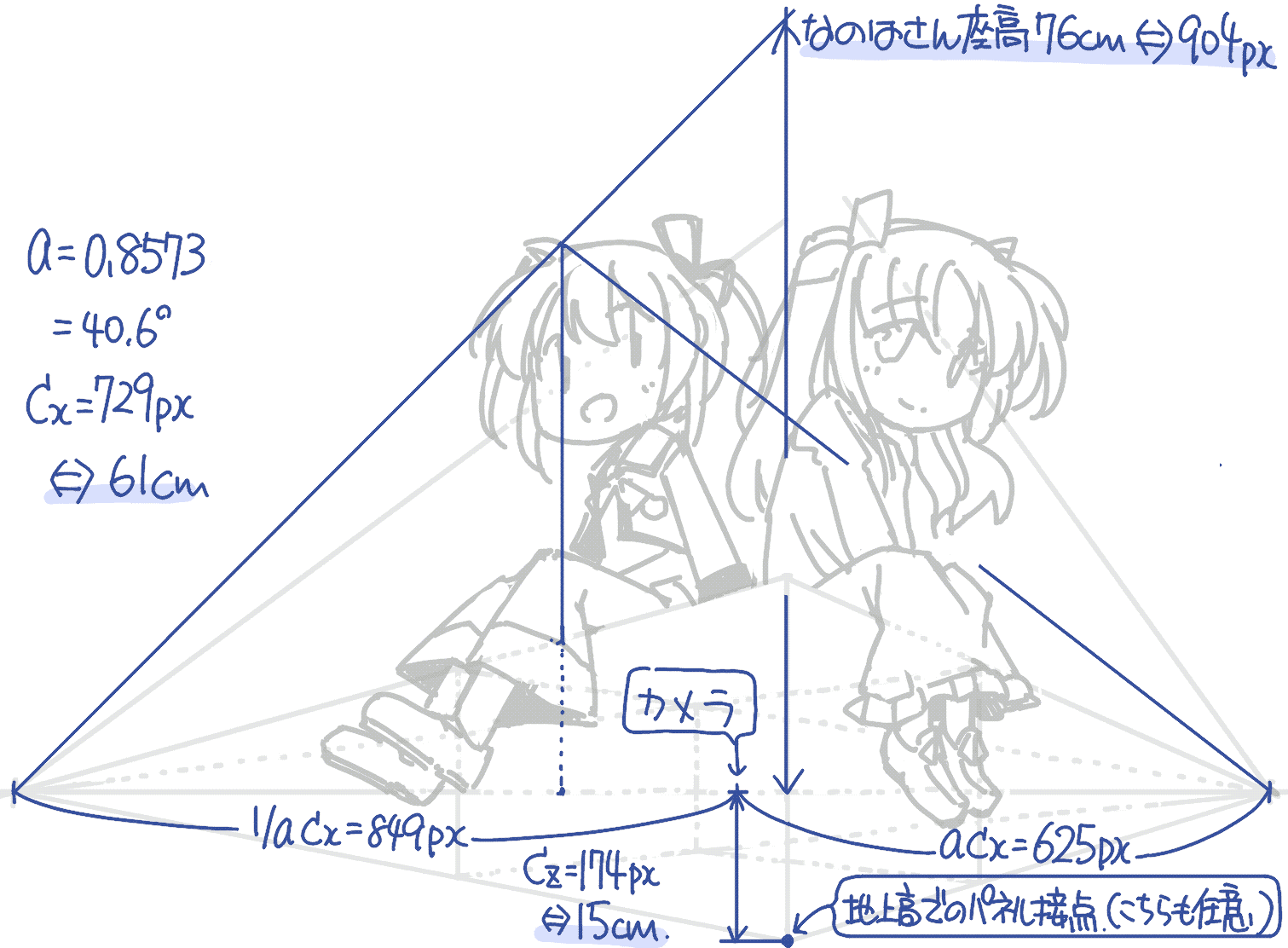
本章では，一点透視の場合に示した45°の場合を一般化して傾きが\(\tan{\theta} = a\)の場合を考えます．

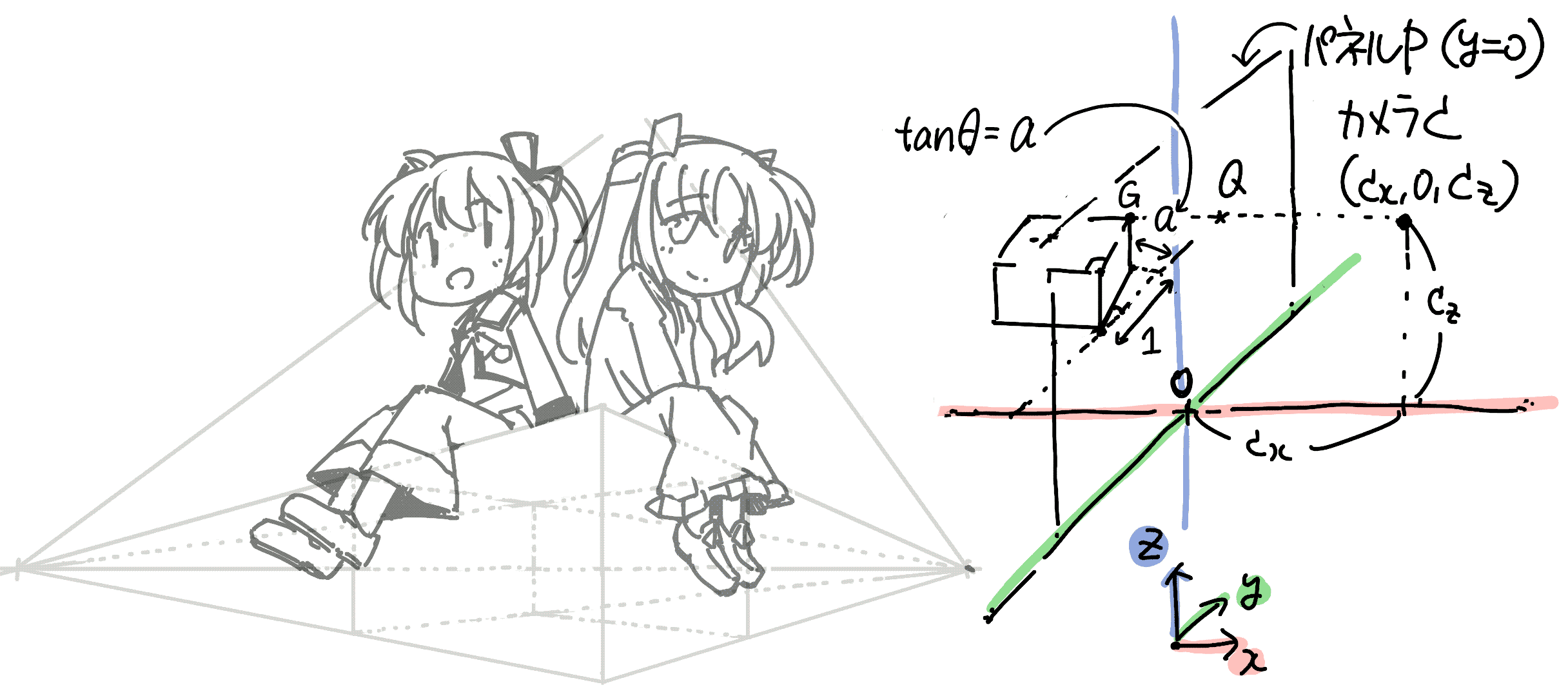
まず， \(g_\mathrm{y}=-ag_\mathrm{x}\)とおくと， \(g_\mathrm{x} \to -\infty\)のとき下式となり，右奥への移動が\(ac_\mathrm{x}\)に収束することがわかります．

\[ \begin{eqnarray*} q_\mathrm{y} &=& -ag_\mathrm{x} + \frac{-a{g_\mathrm{x}}^2}{c_\mathrm{x}-g_\mathrm{x}} \ &=& \frac{-ac_\mathrm{x}}{c_\mathrm{x}/g_\mathrm{x}-1} = ac_\mathrm{x} \end{eqnarray*} \]

反対側は同様に\(\frac{1}{a}{c_\mathrm{x}}\)に収束します．

次に，2点の消失点のあいだにカメラの左右方向の位置を定めます．一点透視の際に45°相当の傾きを任意に定めた操作と同様，これは作図者が任意に定めてかまいません．

最後に，カメラ位置から左右の消失点までの距離\(ac_\mathrm{x}\)と\(\frac{1}{a}{c_\mathrm{x}}\)を実測すれば傾き\(a\)と，カメラの距離\(c_\mathrm{x}\)を計算できます．今回は\(\arctan{a} = 40.6°\)，\(c_\mathrm{x} =729_\mathrm{px} \)となりました．

また，カメラの高さは一点透視の場合と同じく消失点に一致します．

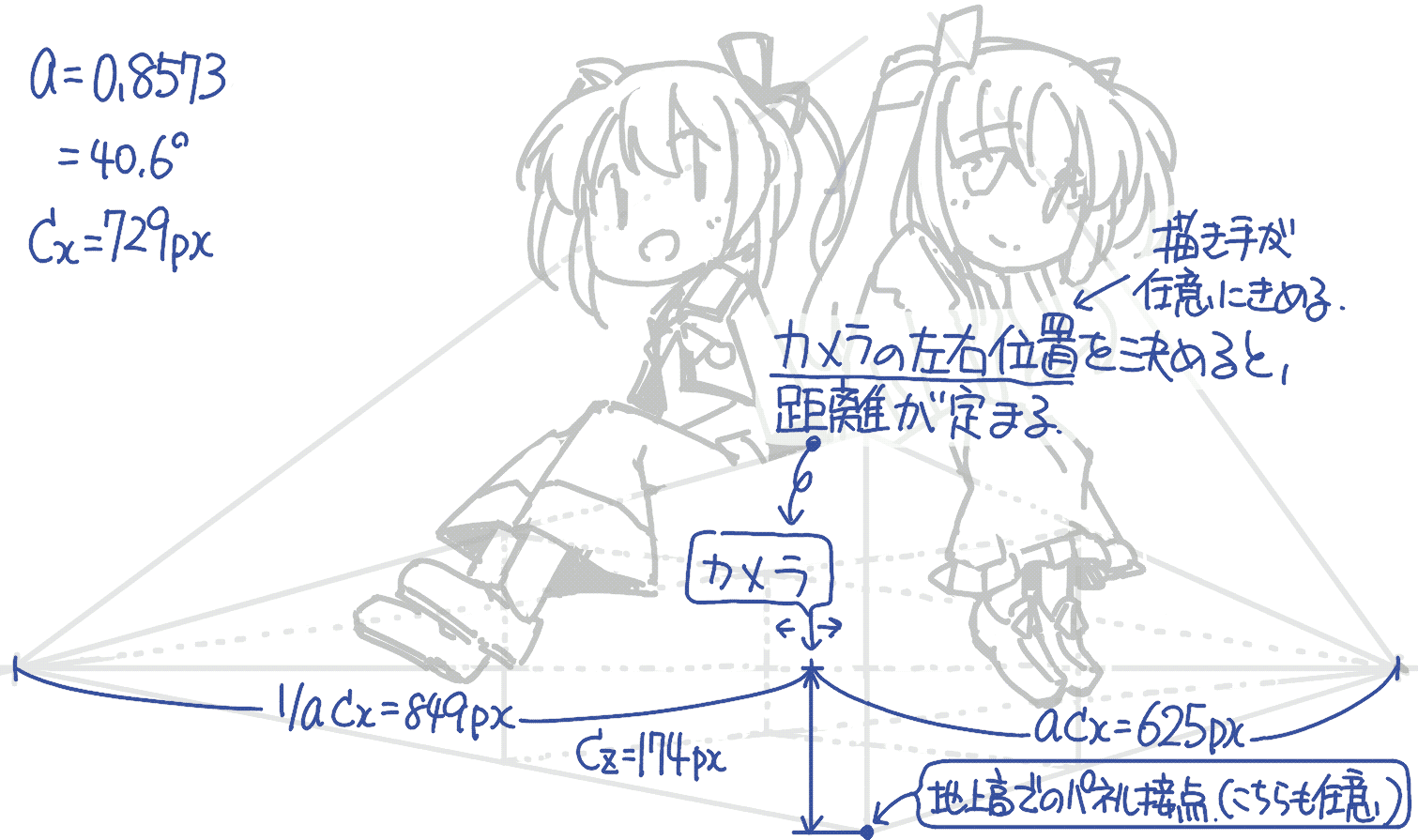
さらに寸法の基準としてなのはさんの座高を76cmと仮定しました．なのはさんが少し奥に座っていますので，パネルと接している箇所(図中で，直方体の手前と定めました)での長さを作図で求めて測定します．今回はパネル面での座高=904pxでしたので，先程のカメラ距離は61cmとなります．また，同様にカメラの高さは15cmとなります．

Blenderでの操作

一点透視の場合と同様に，Blenderでレイアウトします．以下では一点透視と同様の操作を一部省略していますので，一点透視#Blenderでの操作も参照してください．

手順	イメージ
(1) まず一点透視と同様にEmpty要素を配置します．視点を正面に設定した後，左右はカメラをy軸に．上下は，任意に定めたパネルと地面の交点をz軸に合わせます．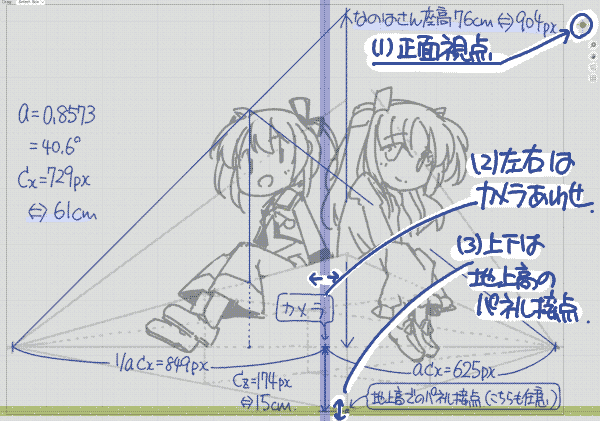
(2) 下描きの拡大率を調整するための基準となるオブジェクトを追加します．今回は76cmと仮定した座高にカメラ高15cmを加えた91cmの柱を設けます．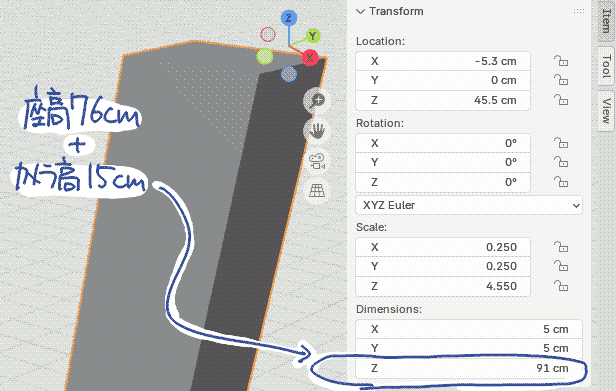
(3) 下描きを拡大操作する際の起点を定めるために，Pivotを3D Cursorに，3D Cursorを原点に設定します．その後，正面視点で高さがパネル面での座高と一致するように拡大します．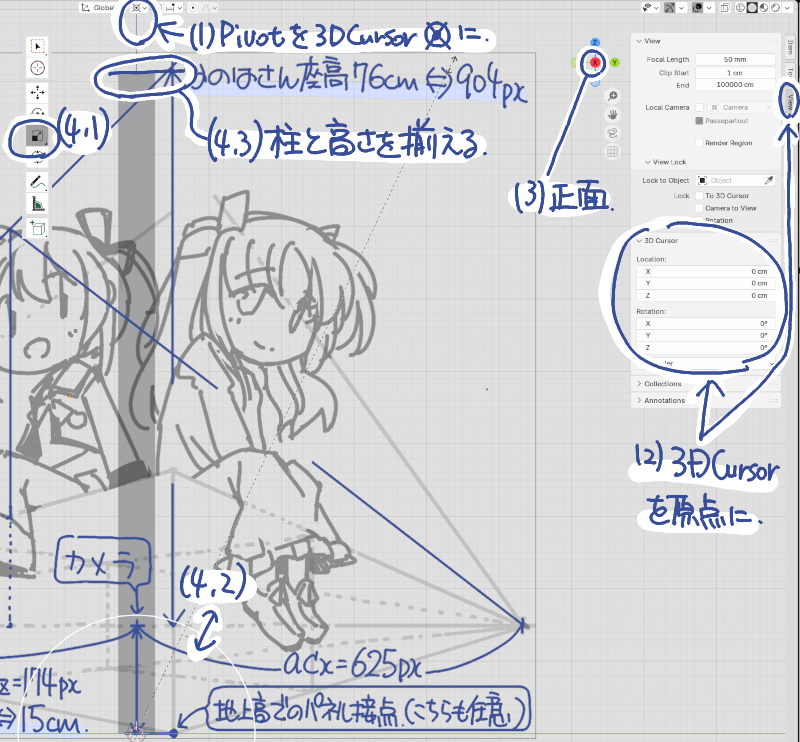
(4) カメラを手前側(x軸)=61cm，高さ(z軸)=15cmに設定します．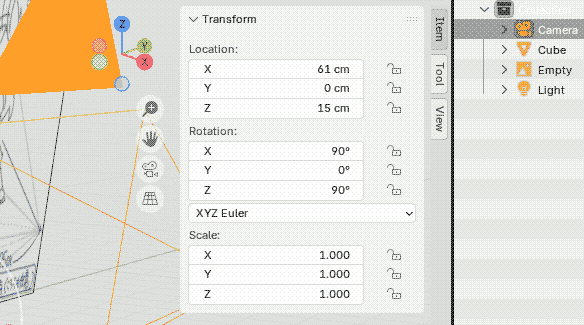
(5) カメラ視点にして，視界を少し調整しておきます．今回はFocal Length=20mm，Shift X=-0.07，Y=0.16に設定しました．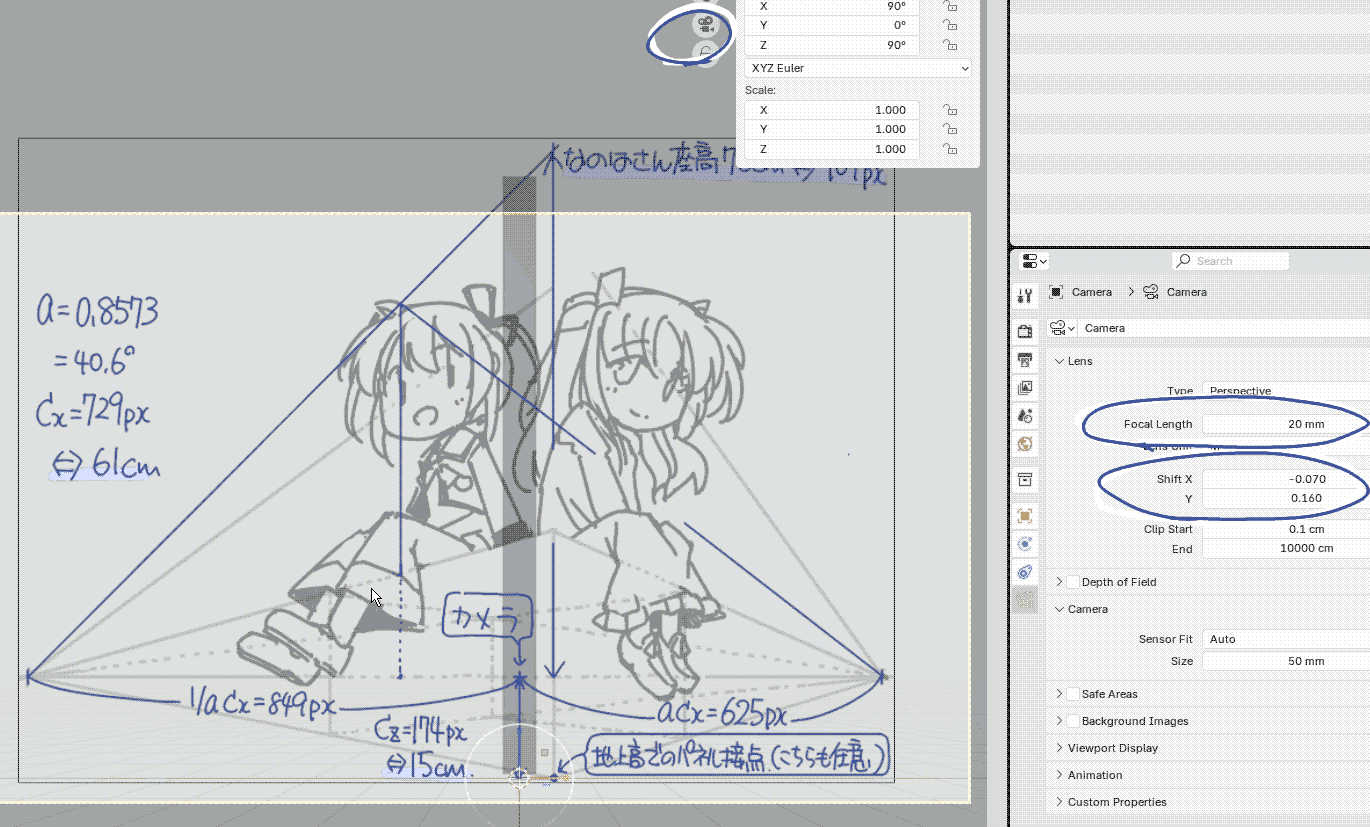
(6) 直方体を追加して40.6°回転した後．少女らが座っている箇所に目測で配置します．なお，回転操作は[r]→[z]→[-40.6]→[Ret]とすると便利です(注:モデルとの整合性のつごうでBlenderでは負方向に回転します．しまった．．)．
(7) 検証として，高さの基準とした78cmの棒をなのはさんの位置に移動すると，おおよそ高さが一致します．また，回転したオブジェクトを奥行方向に拡大すると，それぞれの消失点に向かうことが確認できます．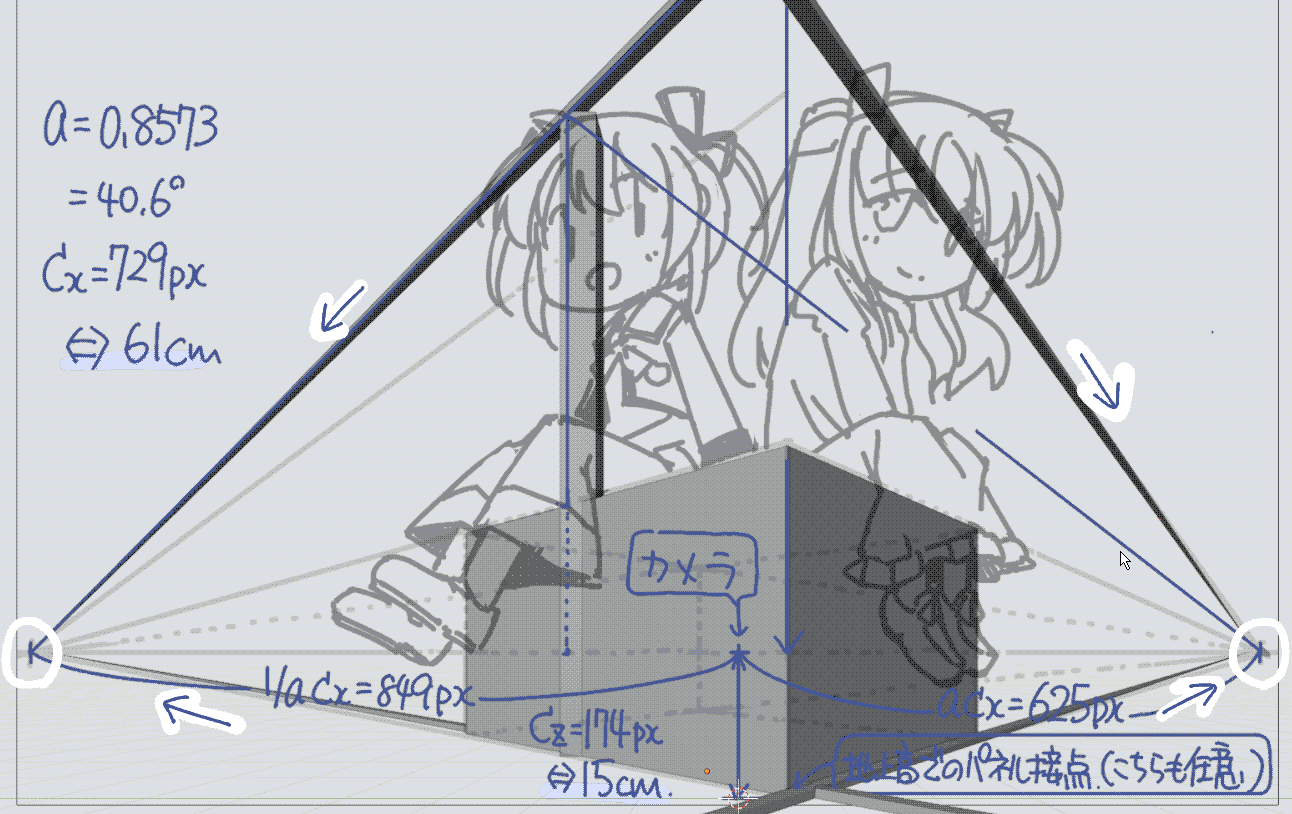

二点透視については以上です．続いて三点透視について説明します．

三点透視

本章では，俯瞰や仰望を表現するためにパネルを傾けることで三点透視を表現する方法を説明します．

以下ではまずモデルの概要を説明します．次にカメラの座標に加えて傾きを算出します．さいごに，寸法の基準とするモデル上の長さとパネルに投影された長さとの対応を説明した後，Blenderでの操作を示します．

モデルの概要

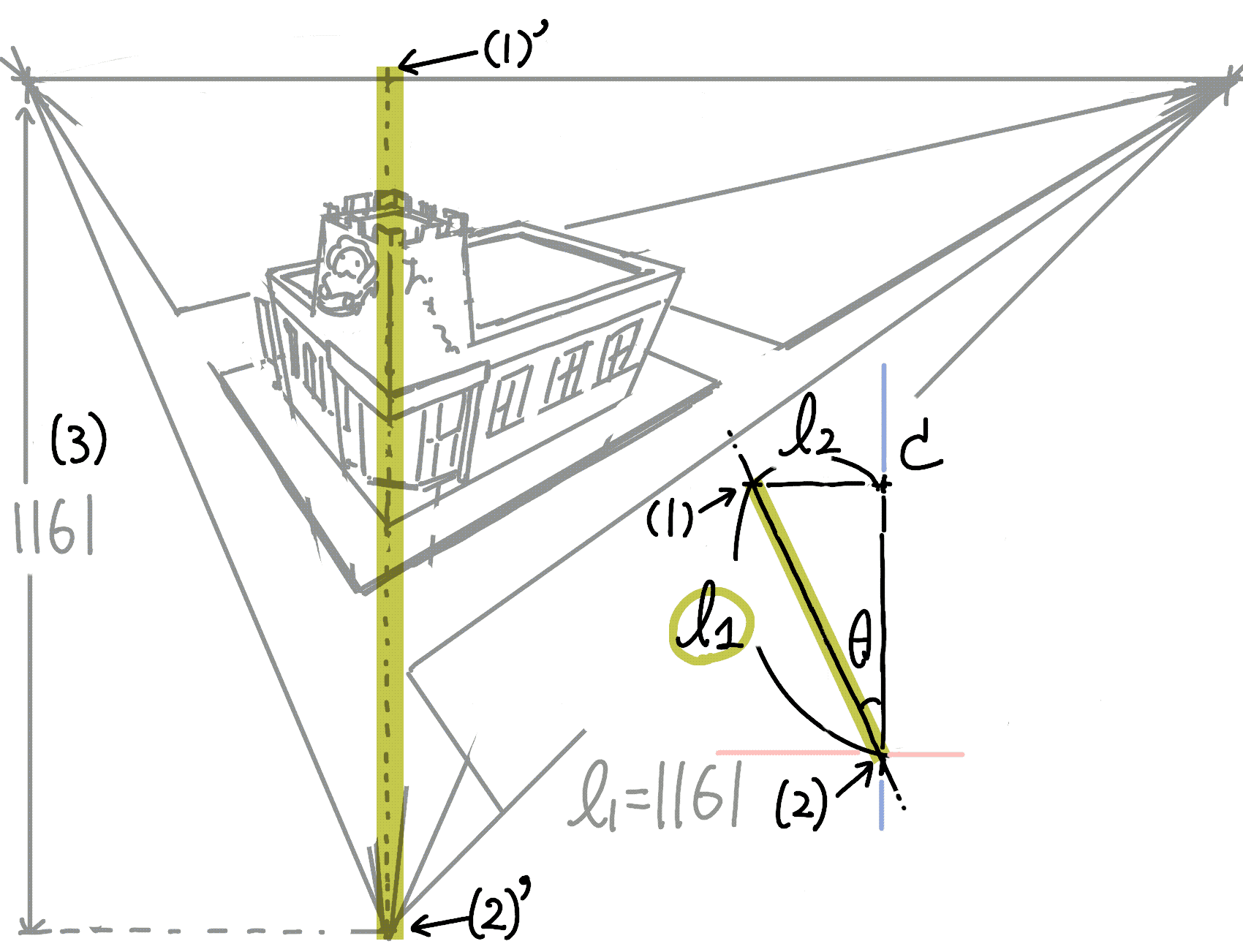
まず，パネルの傾きを\(\theta\)とします．次にカメラからの垂線との交点(=下側の消失点)を原点と考えます．そしてカメラからの水平線とパネルの交点をおいて，そこから原点との距離を\(l_\mathrm{1}\)，カメラとの距離を\(l_\mathrm{2}\)とします．

以下では傾き\(\theta\)を求めるために\(l_\mathrm{1}\)と\(l_\mathrm{2}\)を考えます．

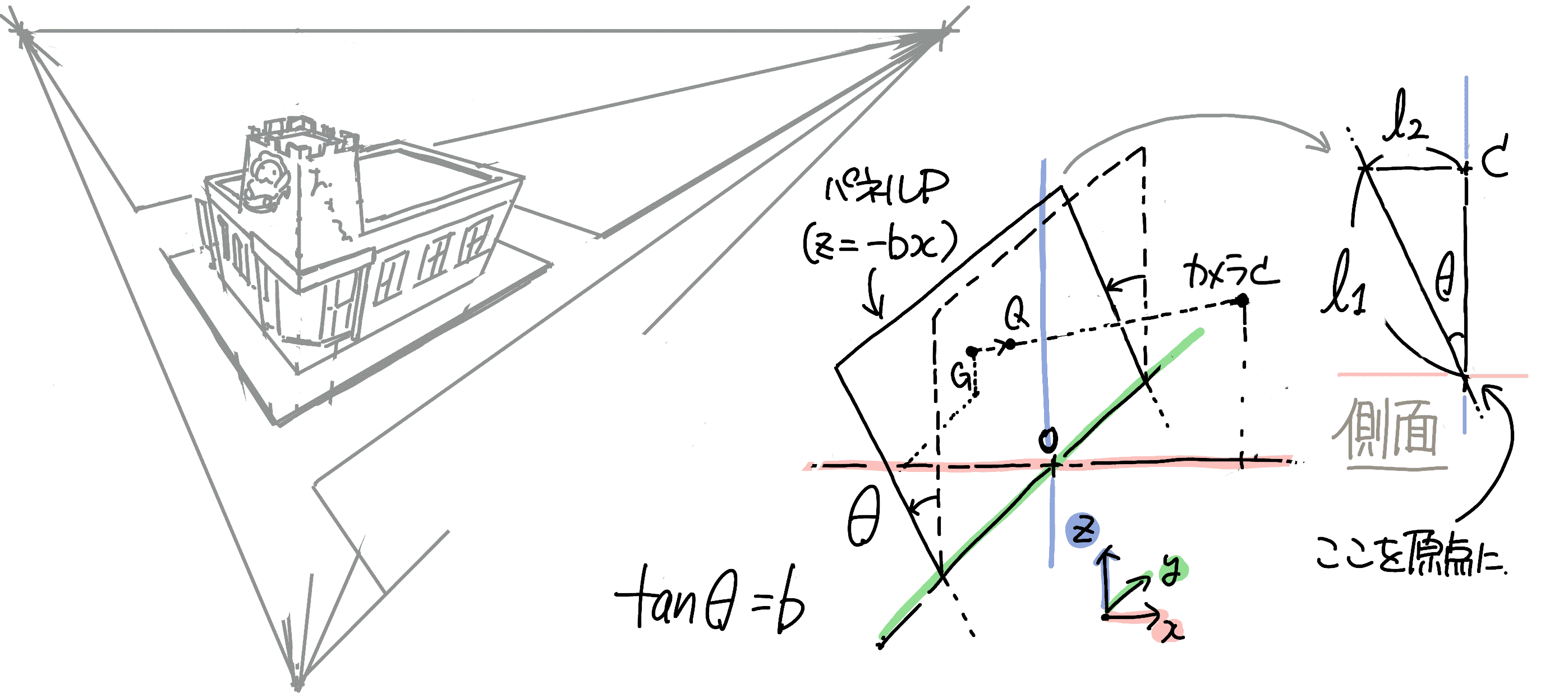
\(l_\mathrm{1}\)の導出

上側は，カメラからの水平線とパネルの交点とします(二点透視と同様)(1)．下側は，カメラからの垂線とパネルの交点とします(下側の消失点)(2)．この長さは，パネル(下描き)上で実測して求めることができます(3)．

\(l_\mathrm{2}\)の計算

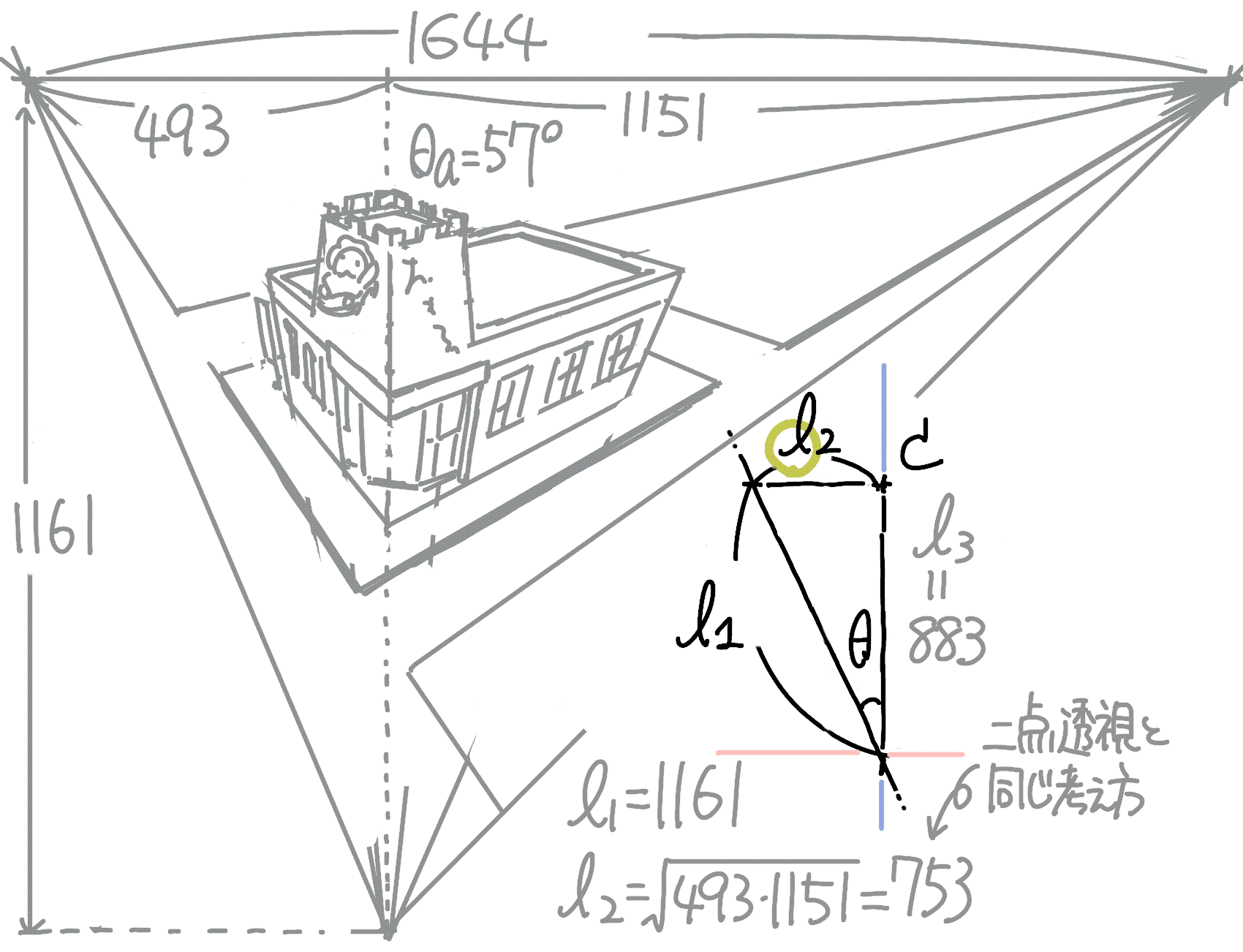
カメラCから水平方向の視界には二点透視と同様のモデルが適用できるので，左右比率を任意に決めるとパネルからカメラまでの距離\(l_\mathrm{2}\)を計算できます．

\(l_2 = \sqrt{493 \cdot 1151} \simeq 753\)

また，\(a=1151/753=1.53\)(=正接)となるので，z軸方向の傾きは約\(57^\circ\)となります．

なお，\(l_\mathrm{1}\)と\(l_\mathrm{2}\)がわかりましたのでカメラの高さは\(l_3 = c_\mathrm{z} \simeq 883\mathrm{[px]}\)となります．

\(\theta\)の計算

前節より，パネルの傾き\(\theta\)は下式となります．

\(\theta = \sin^{-1}\frac{l_2}{l_1} \simeq 40.5^\circ\)．

基準高の換算

寸法合わせの基準となりそうな線分が，パネル上でどのような長さになるかを考えます．ここでは建物の高さSを基準として，この長さとパネル上での長さである\(E_\mathrm{u}\)から\(E_\mathrm{b}\)との対応を計算します．

なお，一点および二点透視と比較して手間がかかりますので，正確な寸法との対応がまずは次節(Blenderでの操作)に進んでいただいて，必要に応じて確認いただくのでもよいと思います．

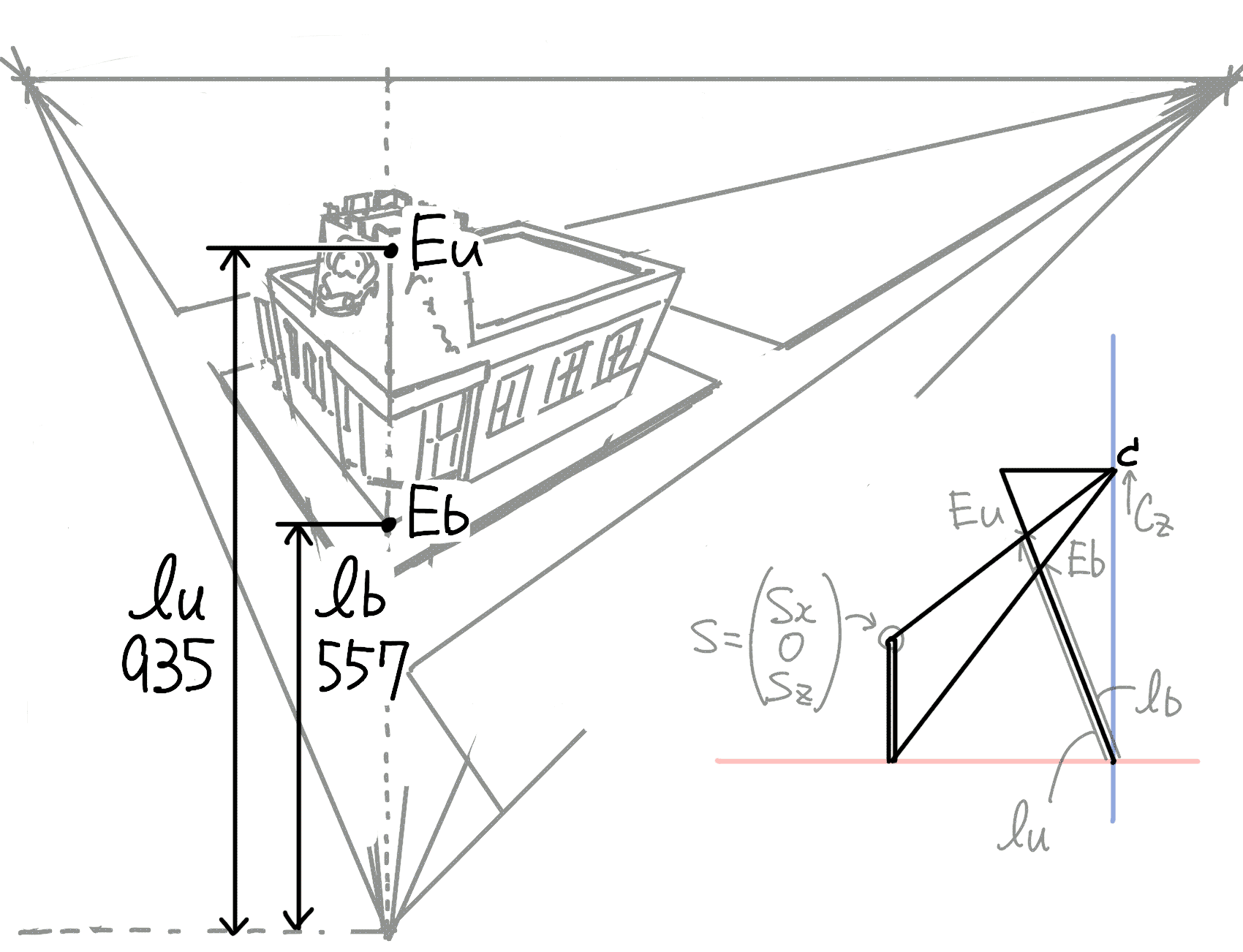
まず\(E_\mathrm{b}\)と\(E_\mathrm{u}\)の座標を求めます．

\[ \begin{eqnarray*} \begin{pmatrix} E_\mathrm{bx} \\ E_\mathrm{bz} \end{pmatrix} = \begin{pmatrix} -l_\mathrm{b} \sin{\theta}\\ l_\mathrm{b} \cos{\theta} \end{pmatrix} \end{eqnarray*} \] \[ \begin{eqnarray*} \begin{pmatrix} E_\mathrm{ux} \\ E_\mathrm{uz} \end{pmatrix} = \begin{pmatrix} -l_\mathrm{u} \sin{\theta}\\ l_\mathrm{u} \cos{\theta} \end{pmatrix} \end{eqnarray*} \]

次に，Sのz座標(\(s_\mathrm{z}\))を求めます．

\(C\)と\(E_\mathrm{b}\)を結ぶ直線とx軸の交点が \(s_\mathrm{x} = -E_\mathrm{bx}\frac{c_\mathrm{z}}{E_\mathrm{bz}-c_\mathrm{z}}\)，その点からの垂線と， \(C\)と\(E_\mathrm{u}\)を結ぶ直線との交点が \(s_\mathrm{z} = -s_\mathrm{x}\frac{c_\mathrm{z}-E_\mathrm{uz}}{E_\mathrm{uz}} + c_\mathrm{z}\) となります．

このとき，既知の値を代入すると，まず\(s_\mathrm{x} = -695\mathrm{[px]}\)がわかります．

これを\(s_\mathrm{z}\)に代入すると\(s_\mathrm{z}=686[\mathrm{px}]\)を得ます．

\(s_\mathrm{z}=686[\mathrm{px}]\)は建物の高さで，仮に\(6[\mathrm{m}]\)とすると，カメラの高さ\(l_\mathrm{3} = c_\mathrm{z} = 883\mathrm{[px]}\)は約\(7.7[\mathrm{m}]\)に対応することになります．よってカメラの高さを7.7[m]に設定して，上側の消失点が一致するように下描きを拡大すれば整合する，と考えられます．また，建物のx座標\(-695\mathrm{[px]}\)は約\(-6.1\mathrm{[m]}\)となります．

または，\(E_\mathrm{uz}-E_\mathrm{bz}=287[\mathrm{px}]=2.51[\mathrm{m}]\)となりますので視点を正面として，そちらで合わせてもよいかもしれません．

Blenderでの操作

手順	イメージ
(1) まず正面視点で下描きのEmpty要素を配置します．今回は下側の消失点を原点としてモデルを策定しましたので，上下左右とも下側の消失点が原点に一致するように調整します．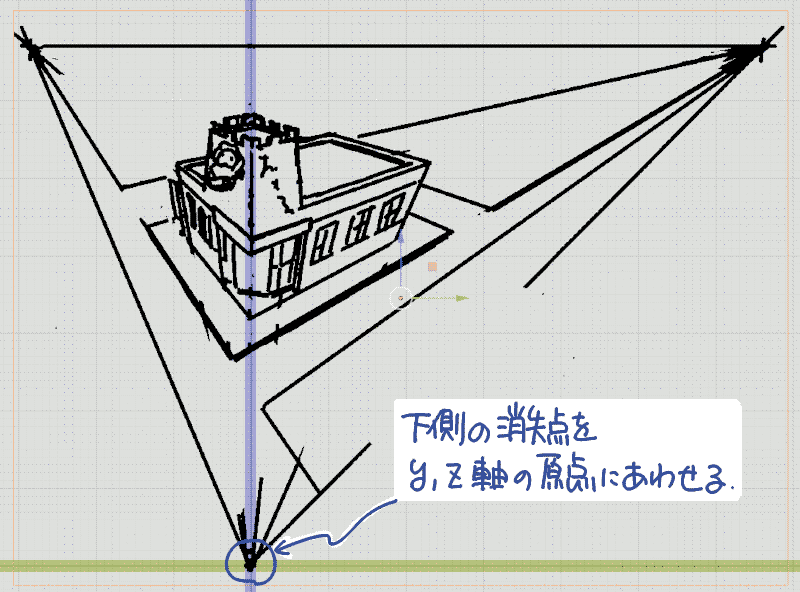
(2) 次に下描きを傾けます．Pivotを原点に設定した3D Cursorとして，Y軸方向に-40.5°傾けます．ショートカットキーを用いる場合は[r]→[y]→[-40.5]→[Ret]となります(負方向に回転)．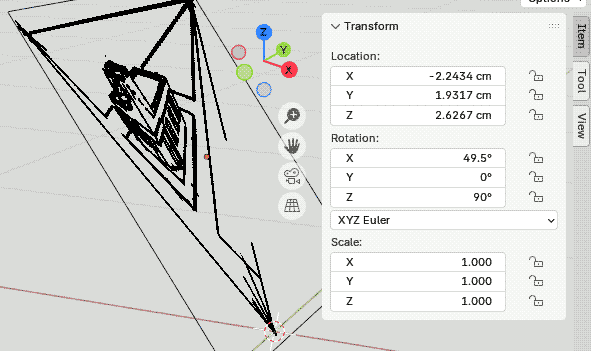
(3) 続いてカメラの位置を設定します．前節で計算したとおり高さl3=883[px]=7.7[m]に設定します．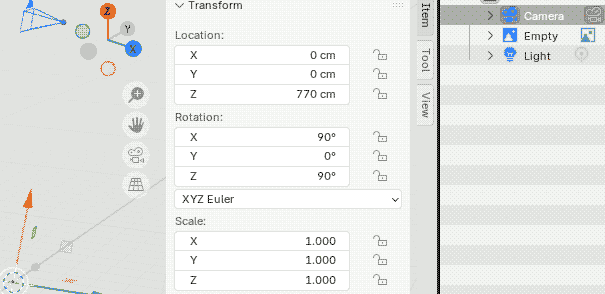
(4) この状態で下描きの拡大率を調整します．正面視点として，下描きの上側消失点を結んだ線分がカメラを横切るように，下描きを座標原点を起点にして拡大します(適宜表示倍率を調整して操作してください．)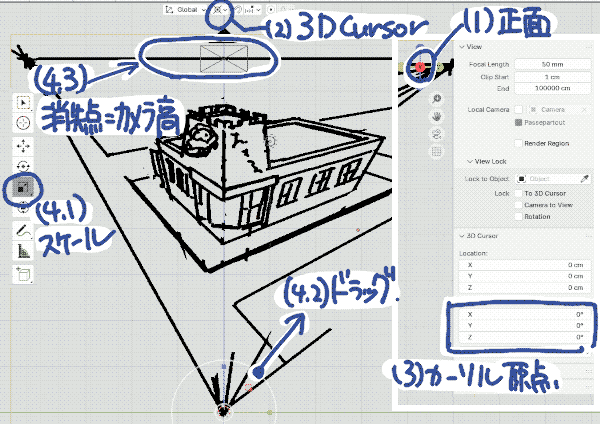
(5) 最後にカメラを回転します．Pivotをバウンディングボックスの中心としたあと，下描きと同様にY軸で40.5°傾けます．また，焦点距離とシフトは適宜調整してください．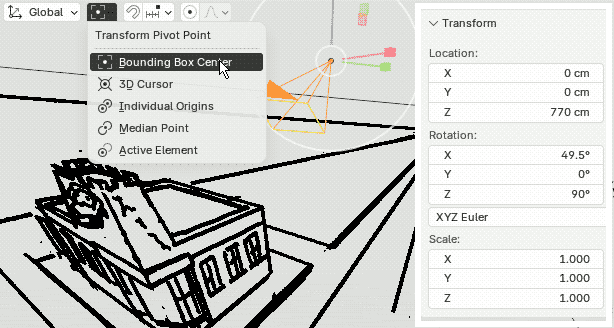
(6) 検証として，高さ6[m]のオブジェクトをx=-6.1[m]に配置するとおおよそ建物に一致します．また，左右奥行きに伸びるオブジェクトを57°の角度で配置するとそれぞれ消失点へ向かうことが確認できます．下方向も同様です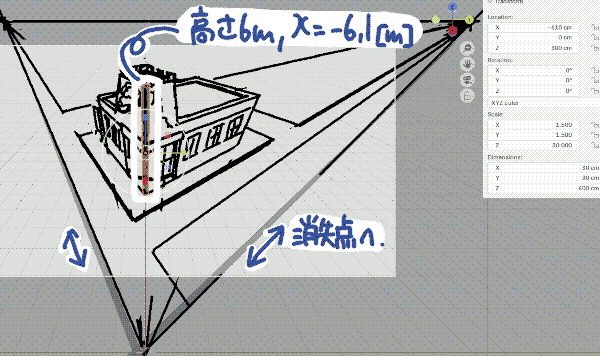

三点透視については以上になります．

まとめと所感

本稿では背景作画の効率化をねらいとして，また，個人的な興味の探求として下描きに対して整合する視点座標を3D CAD上で導出するためのモデルの策定，および Blenderにおける作業手順を紹介しました．

所感としまして，本手順による作画は固い印象になる場合が多いと感じました．自然な見えかた(歪み)や，見栄え，また，時間の都合などもあるので透視図法としての正確性にこだわりすぎず，道具のひとつとして覚えておく，くらいがよさそうかなと思います．

ご清覧いただきどうもありがとうございました．

おくづけ

誤りや改善点がありましたら@kam1610，またはhttps://fwing.net/のフォームよりお知らせいただけましたら幸いです．なるべく修正したいと思いますが手のまわらないこともありますのでその場合はご容赦ください．

本稿はこちらでも公開しています．

改訂メモ

2025-05-02

初版

透視図法の下描きに応じたカメラ座標を算出する方法