二点透視

本章では，一点透視の場合に示した45°の場合を一般化して 傾きが\(\tan{\theta} = a\)の場合を考えます．

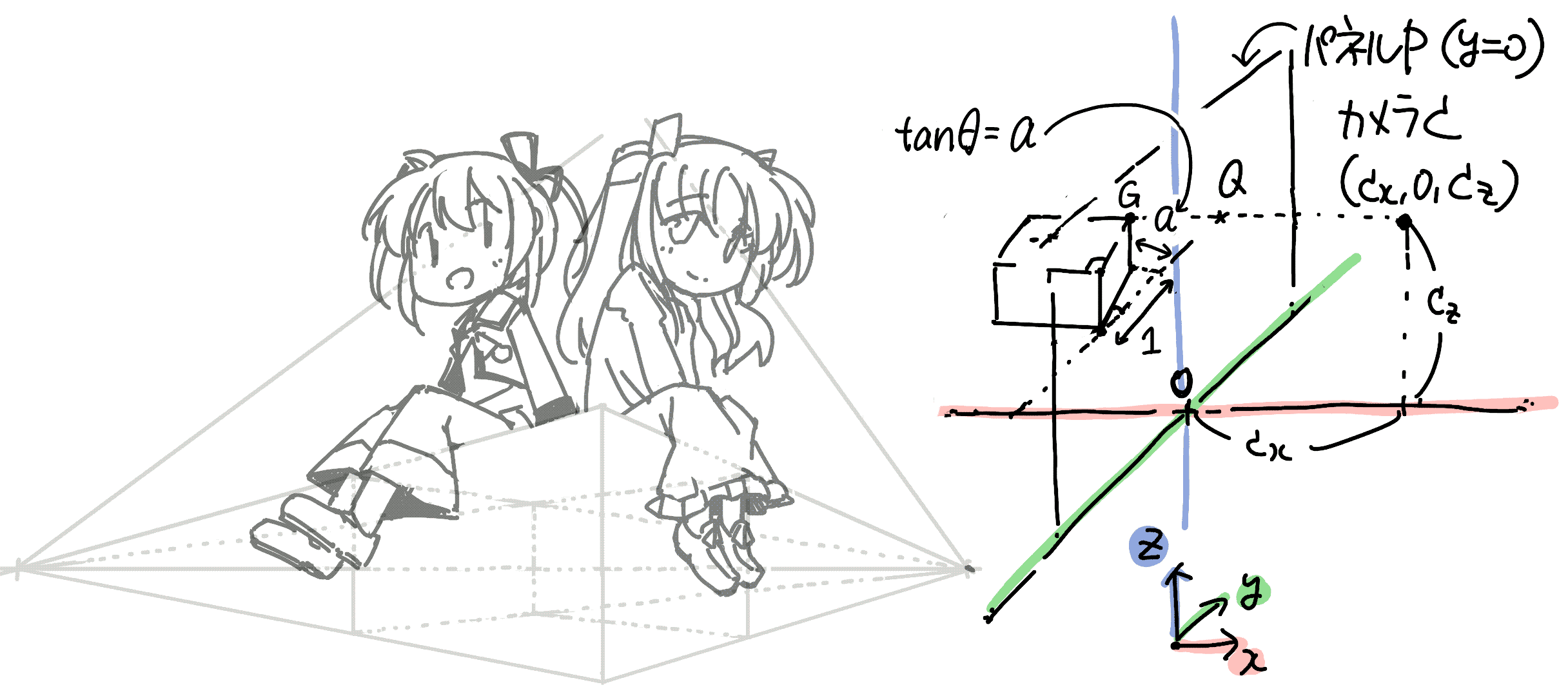
まず， \(g_\mathrm{y}=-ag_\mathrm{x}\)とおくと， \(g_\mathrm{x} \to -\infty\)のとき下式となり， 右奥への移動が\(ac_\mathrm{x}\)に収束することがわかります．

\[ \begin{eqnarray*} q_\mathrm{y} &=& -ag_\mathrm{x} + \frac{-a{g_\mathrm{x}}^2}{c_\mathrm{x}-g_\mathrm{x}} \ &=& \frac{-ac_\mathrm{x}}{c_\mathrm{x}/g_\mathrm{x}-1} = ac_\mathrm{x} \end{eqnarray*} \]

反対側は同様に\(\frac{1}{a}{c_\mathrm{x}}\)に収束します．

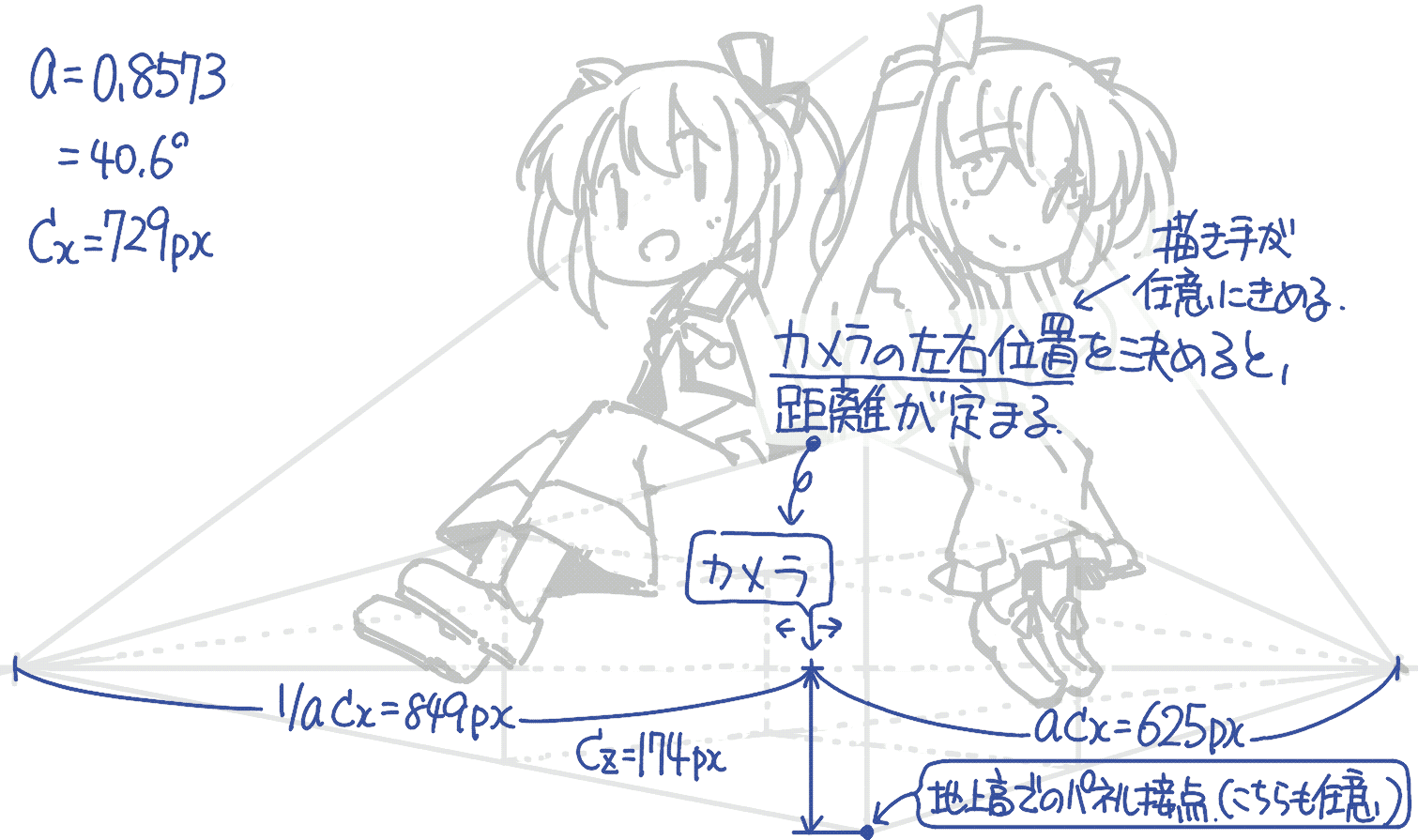
次に，2点の消失点のあいだにカメラの左右方向の位置を定めます． 一点透視の際に45°相当の傾きを任意に定めた操作と同様，これは作図者が任意に定めてかまいません．

最後に，カメラ位置から左右の消失点までの距離\(ac_\mathrm{x}\)と\(\frac{1}{a}{c_\mathrm{x}}\)を実測すれば傾き\(a\)と，カメラの距離\(c_\mathrm{x}\)を計算できます． 今回は\(\arctan{a} = 40.6°\)，\(c_\mathrm{x} =729_\mathrm{px} \)となりました．

また，カメラの高さは一点透視の場合と同じく消失点に一致します．

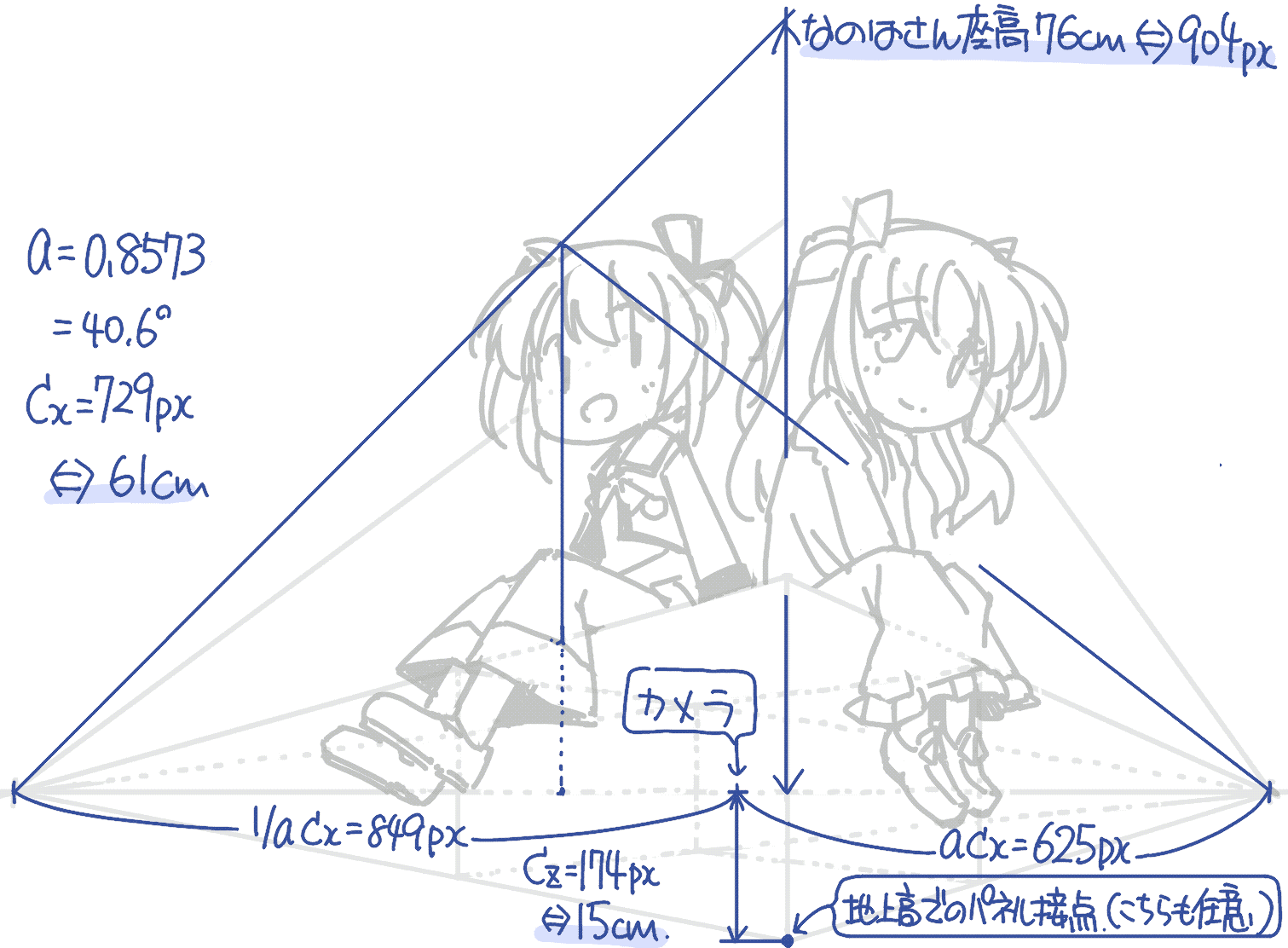
さらに寸法の基準としてなのはさんの座高を76cmと仮定しました．なのはさんが少し奥に座っていますので， パネルと接している箇所(図中で，直方体の手前と定めました)での長さを 作図で求めて測定します．今回はパネル面での座高=904pxでしたので，先程のカメラ距離は61cmとなります． また，同様にカメラの高さは15cmとなります．

Blenderでの操作

一点透視の場合と同様に，Blenderでレイアウトします．以下では一点透視と同様の操作を 一部省略していますので，一点透視#Blenderでの操作も参照してください．

手順	イメージ
(1) まず一点透視と同様にEmpty要素を配置します．視点を正面に設定した後，左右はカメラをy軸に．上下は，任意に定めたパネルと地面の交点をz軸に合わせます．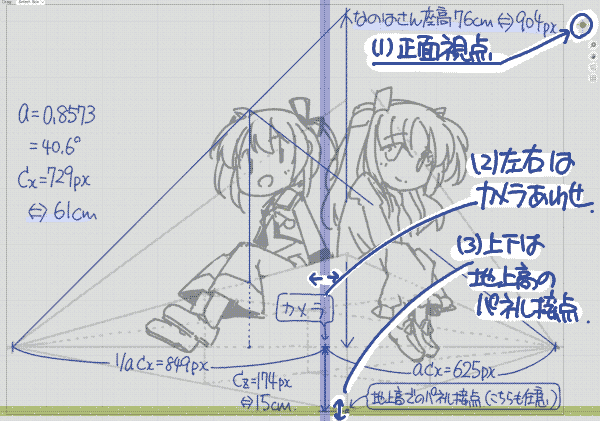
(2) 下描きの拡大率を調整するための基準となるオブジェクトを追加します．今回は76cmと仮定した座高にカメラ高15cmを加えた91cmの柱を設けます．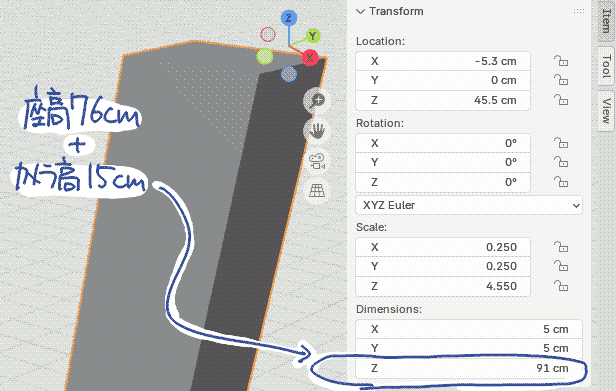
(3) 下描きを拡大操作する際の起点を定めるために，Pivotを3D Cursorに，3D Cursorを原点に設定します．その後，正面視点で高さがパネル面での座高と一致するように拡大します．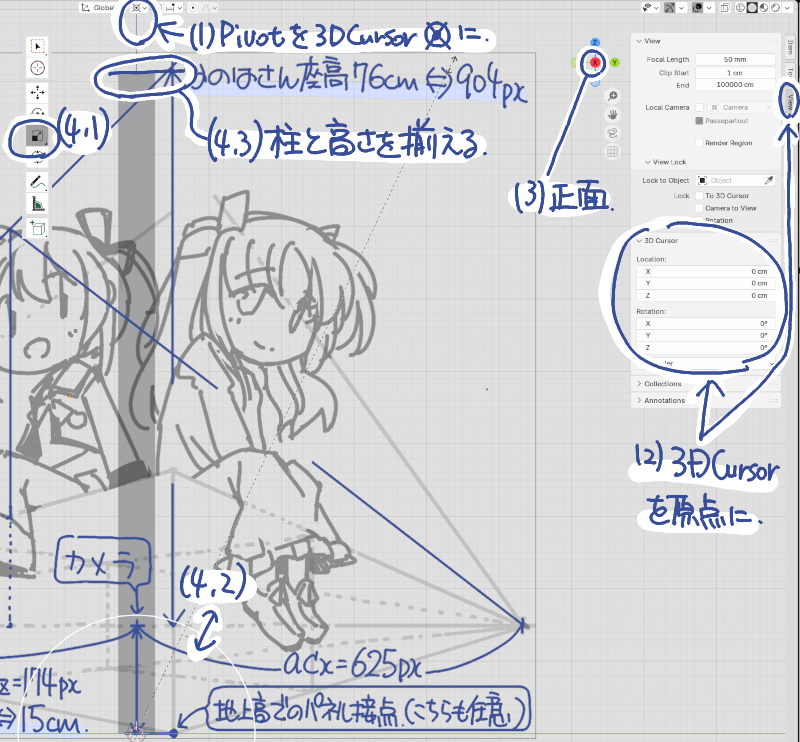
(4) カメラを手前側(x軸)=61cm，高さ(z軸)=15cmに設定します．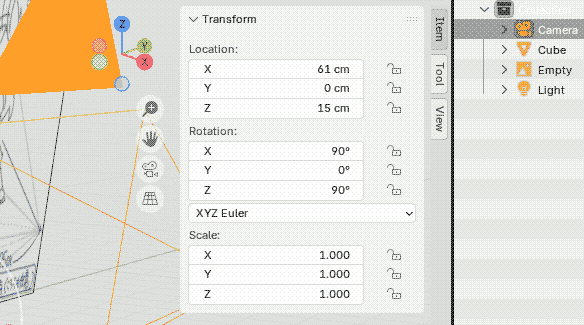
(5) カメラ視点にして，視界を少し調整しておきます．今回はFocal Length=20mm，Shift X=-0.07，Y=0.16に設定しました．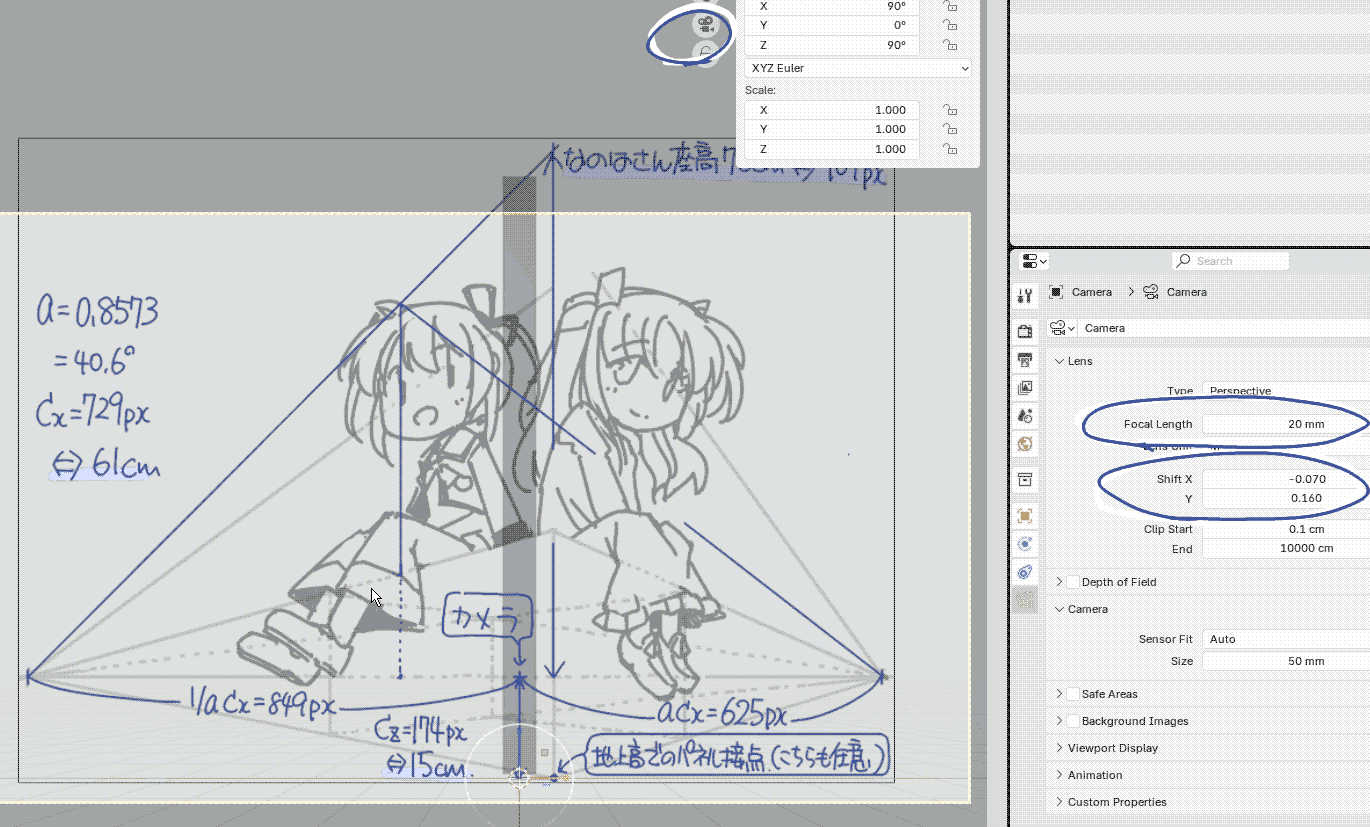
(6) 直方体を追加して40.6°回転した後．少女らが座っている箇所に目測で配置します．なお，回転操作は[r]→[z]→[-40.6]→[Ret]とすると便利です(注:モデルとの整合性のつごうでBlenderでは負方向に回転します．しまった．．)．
(7) 検証として，高さの基準とした78cmの棒をなのはさんの位置に移動すると，おおよそ高さが一致します．また，回転したオブジェクトを奥行方向に拡大すると，それぞれの消失点に向かうことが確認できます．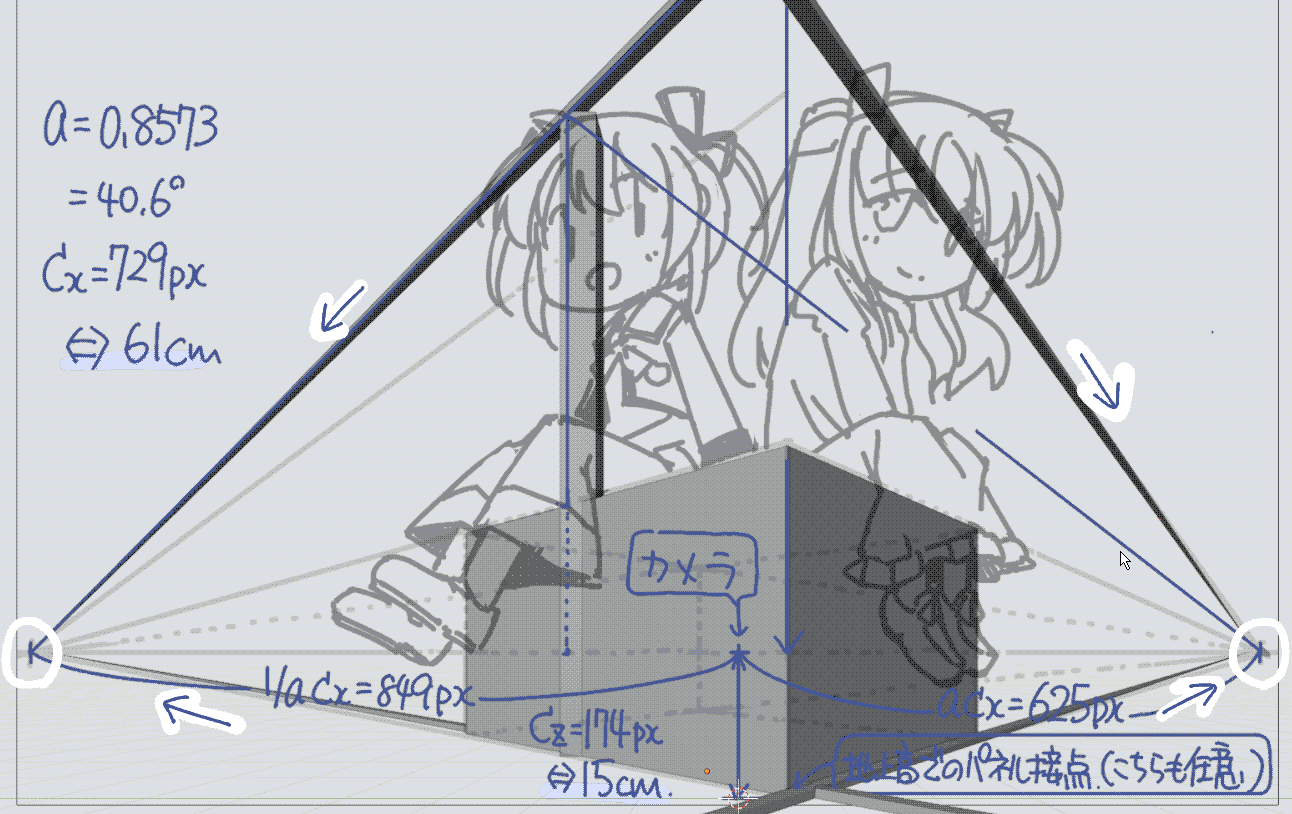

二点透視については以上です．続いて三点透視について説明します．