三点透視

本章では，俯瞰や仰望を表現するためにパネルを傾けることで三点透視を表現する方法を説明します．

以下ではまずモデルの概要を説明します． 次にカメラの座標に加えて傾きを算出します． さいごに，寸法の基準とするモデル上の長さと パネルに投影された長さとの対応を説明した後，Blenderでの操作を示します．

モデルの概要

まず，パネルの傾きを\(\theta\)とします．次にカメラからの垂線との交点(=下側の消失点)を原点と考えます．そしてカメラからの水平線とパネルの交点をおいて，そこから原点との距離を\(l_\mathrm{1}\)， カメラとの距離を\(l_\mathrm{2}\)とします．

以下では傾き\(\theta\)を求めるために\(l_\mathrm{1}\)と\(l_\mathrm{2}\)を考えます．

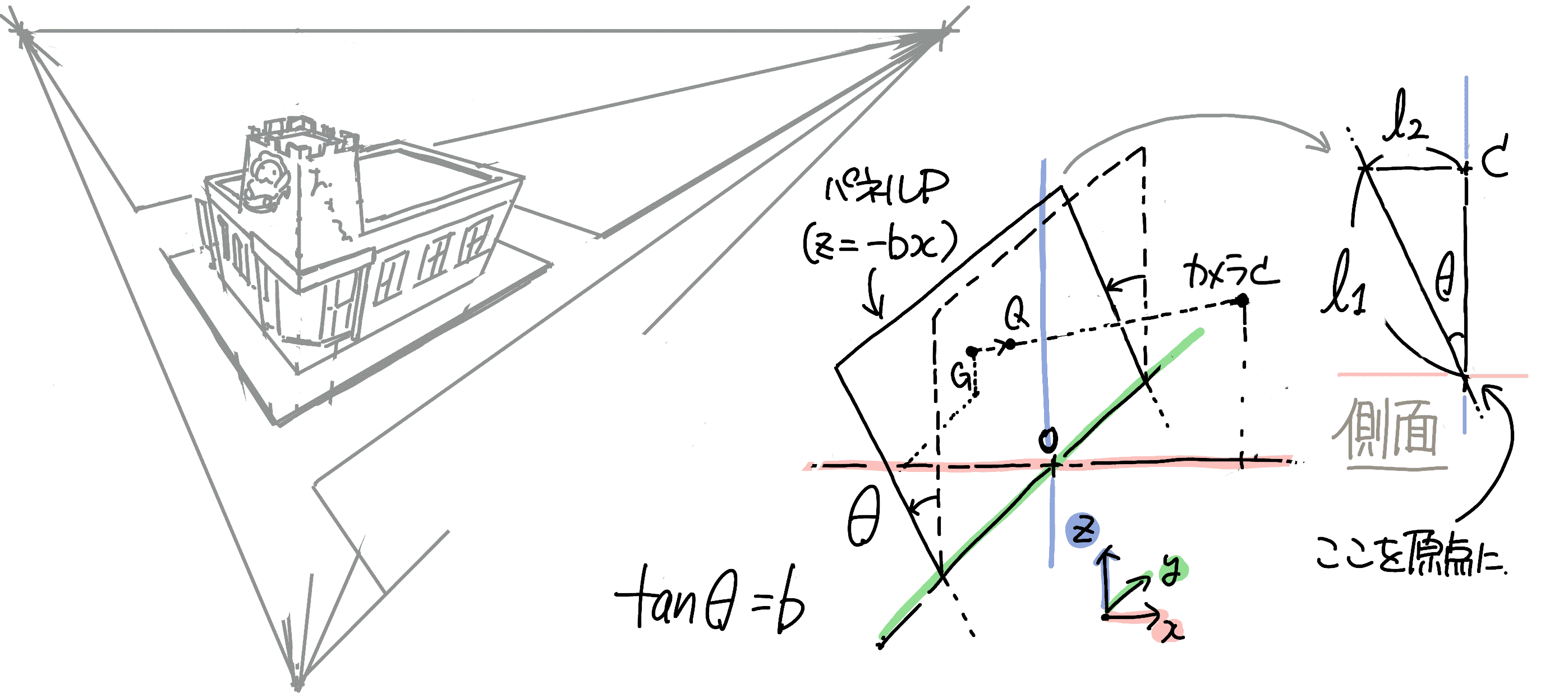
\(l_\mathrm{1}\)の導出

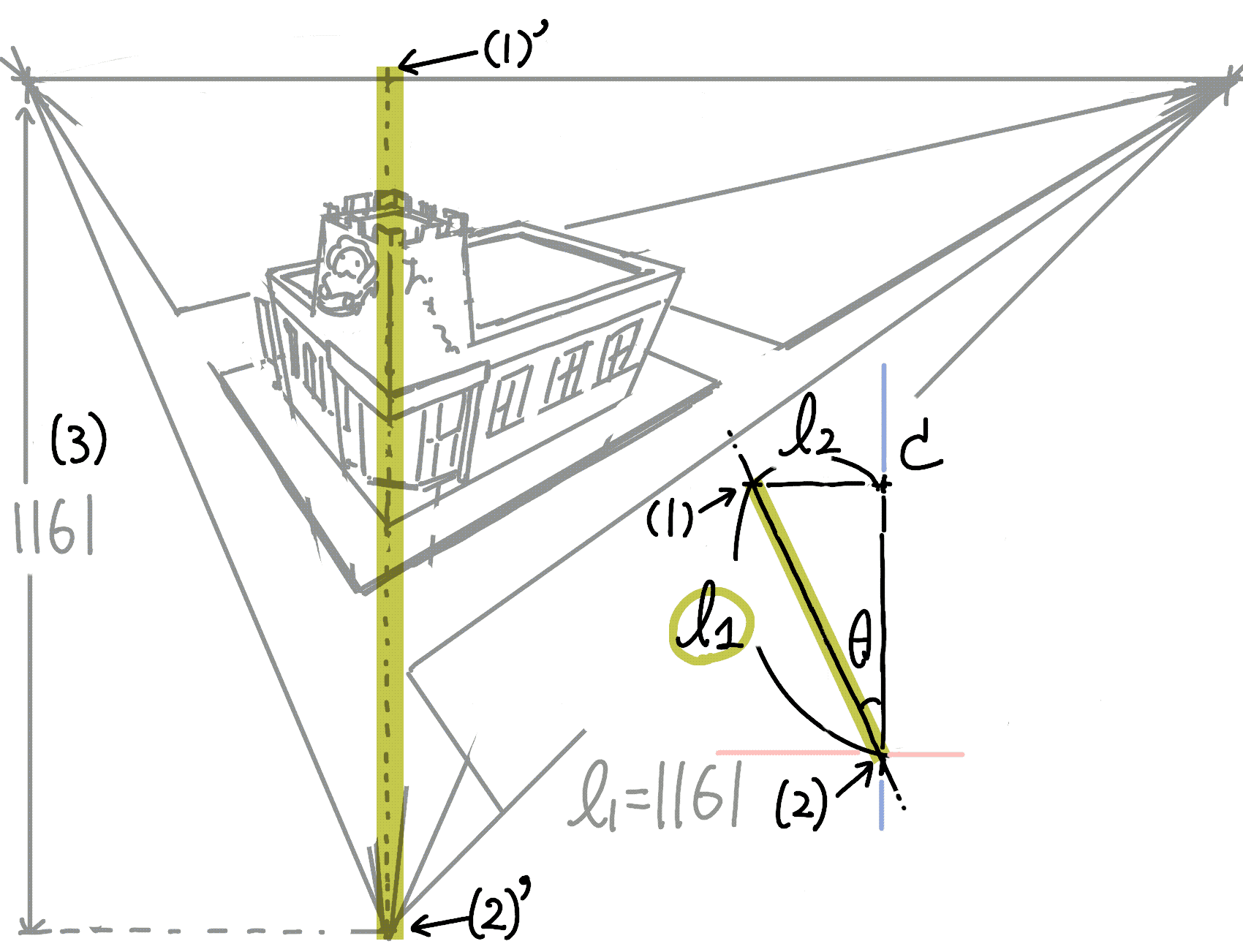
上側は，カメラからの水平線とパネルの交点とします(二点透視と同様)(1)． 下側は，カメラからの垂線とパネルの交点とします(下側の消失点)(2)． この長さは，パネル(下描き)上で実測して求めることができます(3)．

\(l_\mathrm{2}\)の計算

カメラCから水平方向の視界には二点透視と同様のモデルが適用できるので， 左右比率を任意に決めるとパネルからカメラまでの距離\(l_\mathrm{2}\)を計算できます．

\(l_2 = \sqrt{493 \cdot 1151} \simeq 753\)

また，\(a=1151/753=1.53\)(=正接)となるので，z軸方向の傾きは約\(57^\circ\)となります．

なお，\(l_\mathrm{1}\)と\(l_\mathrm{2}\)がわかりましたので カメラの高さは\(l_3 = c_\mathrm{z} \simeq 883\mathrm{[px]}\)となります．

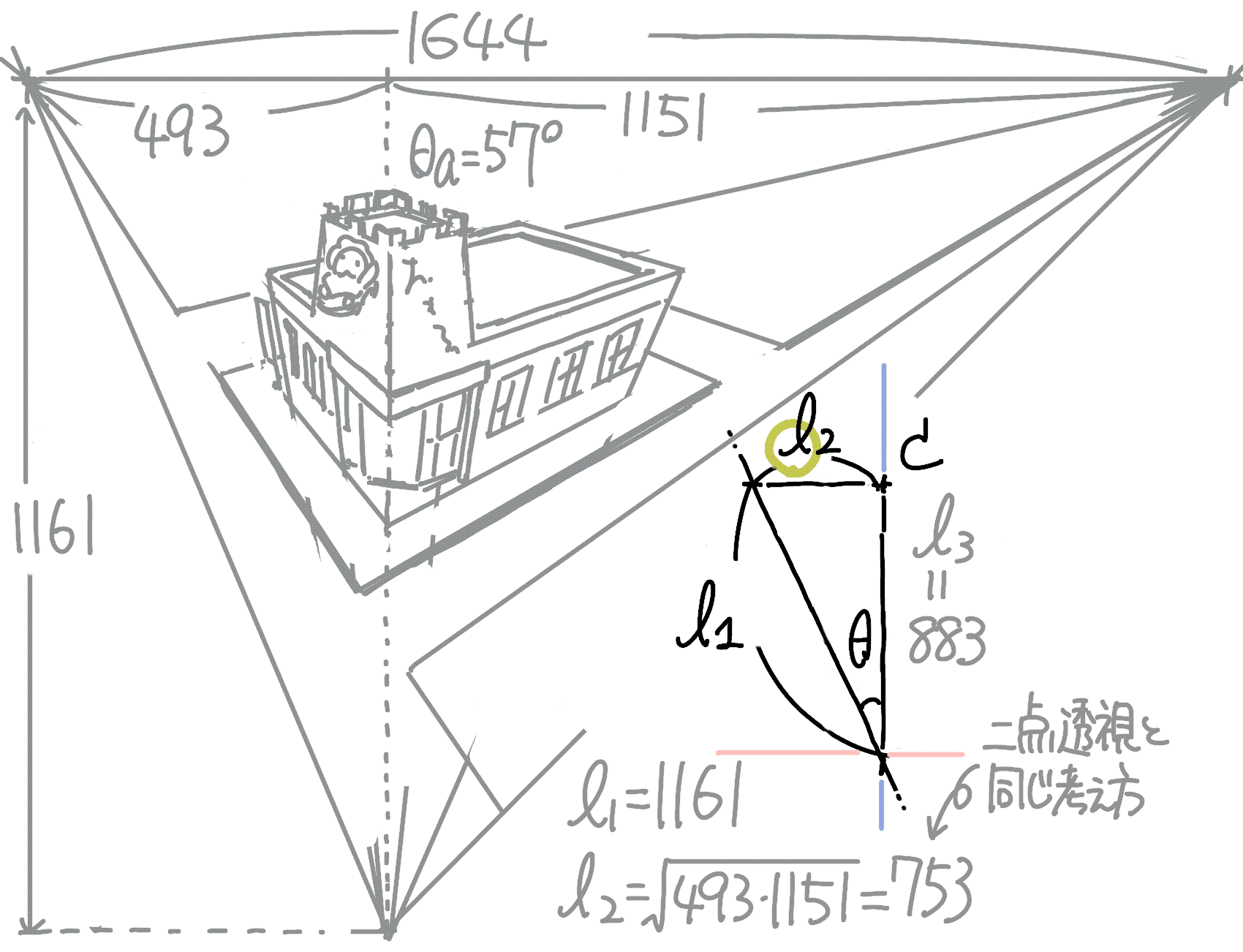
\(\theta\)の計算

前節より，パネルの傾き\(\theta\)は下式となります．

\(\theta = \sin^{-1}\frac{l_2}{l_1} \simeq 40.5^\circ\)．

基準高の換算

寸法合わせの基準となりそうな線分が，パネル上でどのような長さになるかを考えます． ここでは建物の高さSを基準として，この長さと パネル上での長さである\(E_\mathrm{u}\)から\(E_\mathrm{b}\)との対応を計算します．

なお，一点および二点透視と比較して手間がかかりますので，正確な寸法との対応が まずは次節(Blenderでの操作)に進んでいただいて， 必要に応じて確認いただくのでもよいと思います．

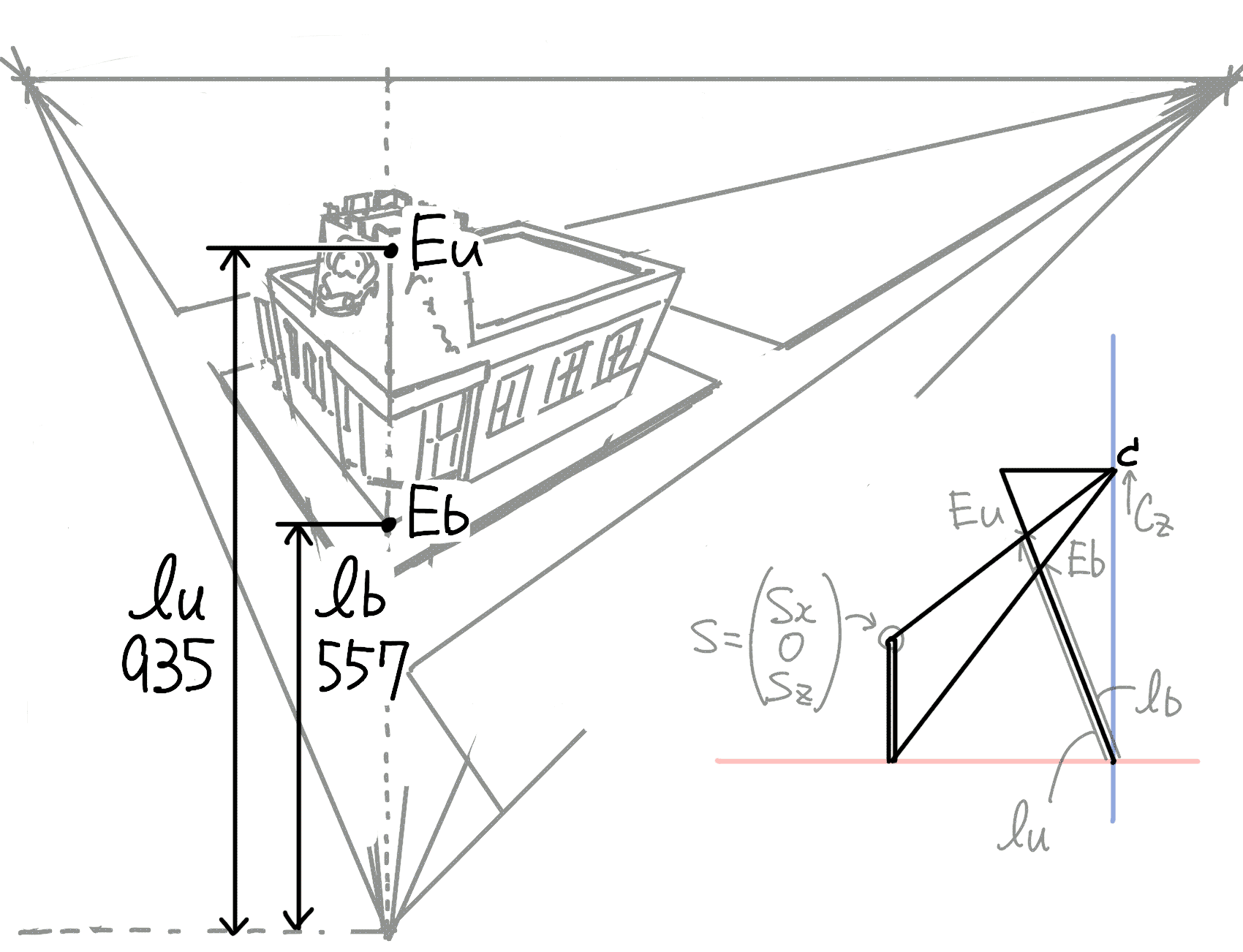
まず\(E_\mathrm{b}\)と\(E_\mathrm{u}\)の座標を求めます．

\[ \begin{eqnarray*} \begin{pmatrix} E_\mathrm{bx} \\ E_\mathrm{bz} \end{pmatrix} = \begin{pmatrix} -l_\mathrm{b} \sin{\theta}\\ l_\mathrm{b} \cos{\theta} \end{pmatrix} \end{eqnarray*} \] \[ \begin{eqnarray*} \begin{pmatrix} E_\mathrm{ux} \\ E_\mathrm{uz} \end{pmatrix} = \begin{pmatrix} -l_\mathrm{u} \sin{\theta}\\ l_\mathrm{u} \cos{\theta} \end{pmatrix} \end{eqnarray*} \]

次に，Sのz座標(\(s_\mathrm{z}\))を求めます．

\(C\)と\(E_\mathrm{b}\)を結ぶ直線とx軸の交点が \(s_\mathrm{x} = -E_\mathrm{bx}\frac{c_\mathrm{z}}{E_\mathrm{bz}-c_\mathrm{z}}\)， その点からの垂線と， \(C\)と\(E_\mathrm{u}\)を結ぶ直線との交点が \(s_\mathrm{z} = -s_\mathrm{x}\frac{c_\mathrm{z}-E_\mathrm{uz}}{E_\mathrm{uz}} + c_\mathrm{z}\) となります．

このとき，既知の値を代入すると，まず\(s_\mathrm{x} = -695\mathrm{[px]}\)がわかります．

これを\(s_\mathrm{z}\)に代入すると\(s_\mathrm{z}=686[\mathrm{px}]\)を得ます．

\(s_\mathrm{z}=686[\mathrm{px}]\)は建物の高さで， 仮に\(6[\mathrm{m}]\)とすると， カメラの高さ\(l_\mathrm{3} = c_\mathrm{z} = 883\mathrm{[px]}\)は 約\(7.7[\mathrm{m}]\)に対応することになります． よってカメラの高さを7.7[m]に設定して， 上側の消失点が一致するように下描きを拡大すれば整合する， と考えられます． また，建物のx座標\(-695\mathrm{[px]}\)は約\(-6.1\mathrm{[m]}\)となります．

または，\(E_\mathrm{uz}-E_\mathrm{bz}=287[\mathrm{px}]=2.51[\mathrm{m}]\)となりますので 視点を正面として，そちらで合わせてもよいかもしれません．

Blenderでの操作

手順	イメージ
(1) まず正面視点で下描きのEmpty要素を配置します．今回は下側の消失点を原点としてモデルを策定しましたので，上下左右とも下側の消失点が原点に一致するように調整します．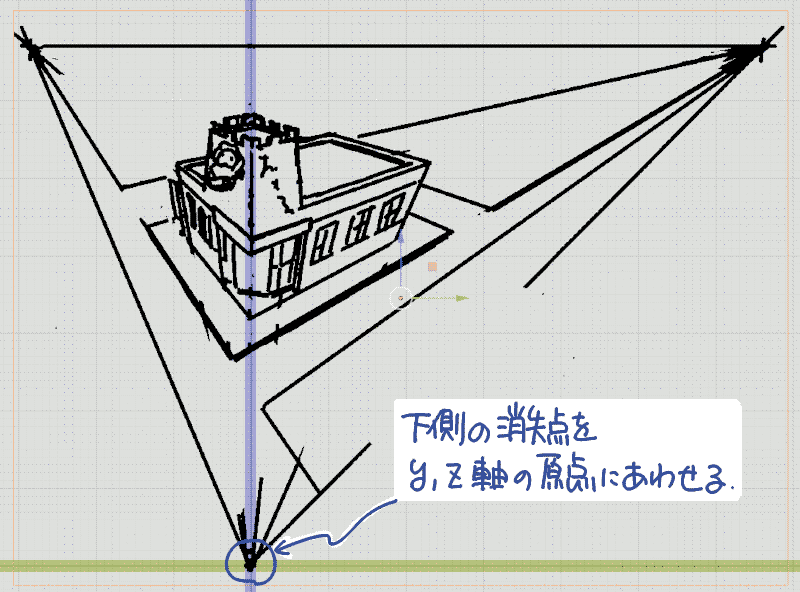
(2) 次に下描きを傾けます．Pivotを原点に設定した3D Cursorとして，Y軸方向に-40.5°傾けます．ショートカットキーを用いる場合は[r]→[y]→[-40.5]→[Ret]となります(負方向に回転)．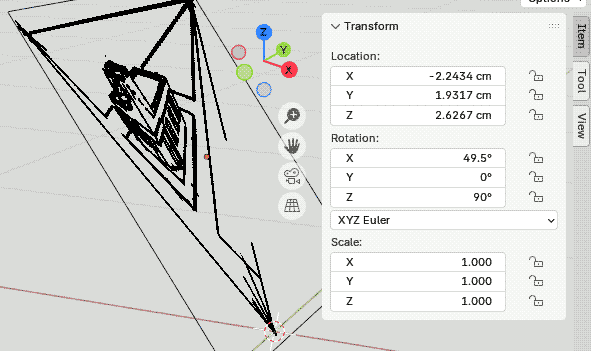
(3) 続いてカメラの位置を設定します．前節で計算したとおり高さl3=883[px]=7.7[m]に設定します．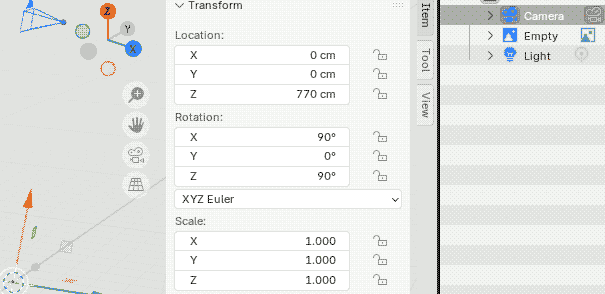
(4) この状態で下描きの拡大率を調整します．正面視点として，下描きの上側消失点を結んだ線分がカメラを横切るように，下描きを座標原点を起点にして拡大します(適宜表示倍率を調整して操作してください．)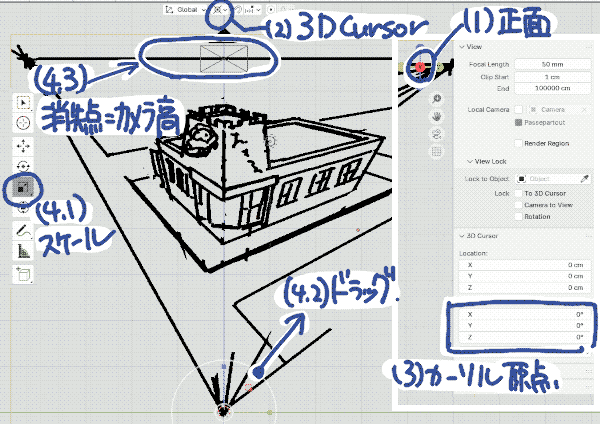
(5) 最後にカメラを回転します．Pivotをバウンディングボックスの中心としたあと，下描きと同様にY軸で40.5°傾けます．また，焦点距離とシフトは適宜調整してください．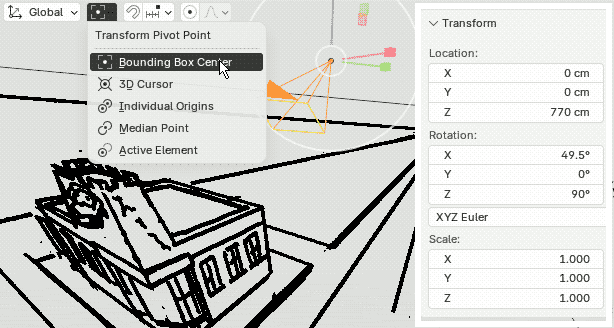
(6) 検証として，高さ6[m]のオブジェクトをx=-6.1[m]に配置するとおおよそ建物に一致します．また，左右奥行きに伸びるオブジェクトを57°の角度で配置するとそれぞれ消失点へ向かうことが確認できます．下方向も同様です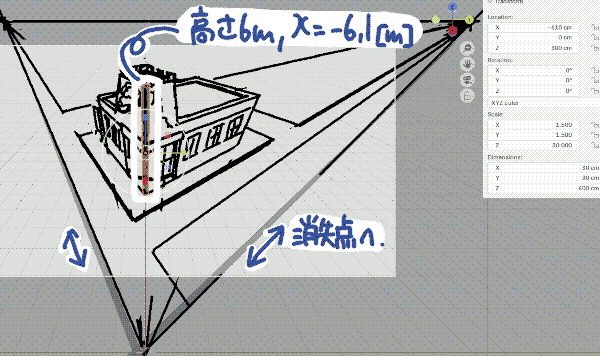

三点透視については以上になります．